题目内容
某单位用木料制作如图所示的框架,框架的下部是边长分别为x、y(单位:m)的矩形,上部是等腰直角三角形,要求框架围成的总面积为8m2,问x、y分别为多少时用料最省?(精确到0.001m) 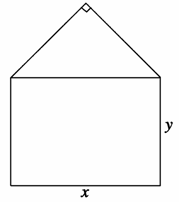
依题意,有xy+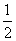 x·
x· =8,
=8,
∴y= =
= -
- (0<x<4
(0<x<4 ),
),
于是框架用料长度为l=2x+2y+2× =
= x+
x+ ,l′=
,l′= +
+ -
- ,
,
令l′=0,即 +
+ -
- =0,解得x1=8-4
=0,解得x1=8-4 ,x2=4
,x2=4 -8(舍去),
-8(舍去),
当0<x<8-4 时,l′<0;当8-4
时,l′<0;当8-4 <x<4
<x<4 时,l′>0;
时,l′>0;
所以当x=8-4 时,l取得最小值,此时,x=8-4
时,l取得最小值,此时,x=8-4 ≈2.343m,y≈2.828m.
≈2.343m,y≈2.828m.
即当x约为2.343m,y约为2.828m时,用料最省.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
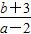 的取值范围是( )
的取值范围是( )
 ,3)
,3) B.
B. 
 D.
D. 

 sinxdx,则二项式(a
sinxdx,则二项式(a -
- )6展开式的常数项等于________.
)6展开式的常数项等于________. 中,已知
中,已知 =
= ,
, =
= ,
, 为
为 边的中点,则下列向量与
边的中点,则下列向量与 同向的是
同向的是 B.
B.  C.
C.  D.
D. 