题目内容
4.一个三棱锥的三视图如图所示,则该三棱锥的表面积为( )
| A. | 2+2$\sqrt{5}$+$\sqrt{14}$ | B. | 16+2$\sqrt{14}$ | C. | 8+2$\sqrt{14}$ | D. | 8+$\sqrt{14}$ |
分析 由题意作图,从而求各个三角形的面积即可.
解答 解:由题意作图如右,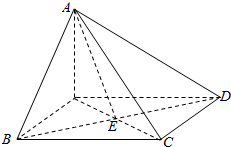
△ABC与△ADC是全等的直角三角形,
其中AB=$\sqrt{5+4}$=3,BC=2,
故S△ADC=S△ABC=$\frac{1}{2}$×2×3=3,
△BDC是等腰直角三角形,
BC=CD=2,
故S△BCD=$\frac{1}{2}$×2×2=2,
△ADB是等腰三角形,
AB=AD=3,BD=2$\sqrt{2}$,
故点A到BD的距离AE=$\sqrt{{3}^{2}-2}$=$\sqrt{7}$,
故S△BAD=$\frac{1}{2}$×2$\sqrt{2}$×$\sqrt{7}$=$\sqrt{14}$,
故表面积S=3+3+2+$\sqrt{14}$=8+$\sqrt{14}$,
故选:D.
点评 本题考查了学生的空间想象力与数形结合的思想应用.

练习册系列答案
相关题目
19.已知O为坐标原点,A,B两点的坐标均满足不等式组$\left\{\begin{array}{l}{x-3y+1≤0}\\{x+y-3≤0}\\{x-1≥0}\end{array}\right.$,设$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为θ,则sinθ的最大值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{4\sqrt{65}}{65}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
16.如图的程序框图表示算法的运行结果是( )


| A. | -2 | B. | 2 | C. | -1 | D. | 1 |
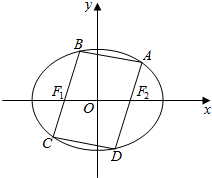 如图,已知四边形ABCD是椭圆3x2+4y2=12的内接平行四边形,且BC,AD分别经过椭圆的焦点F1,F2.
如图,已知四边形ABCD是椭圆3x2+4y2=12的内接平行四边形,且BC,AD分别经过椭圆的焦点F1,F2.