Question

8．某机构为了解某地区中学生在校月消费情况，随机抽取了100名中学生进行调查．右图是根据调查的结果绘制的学生在校月消费金额的频率分布直方图：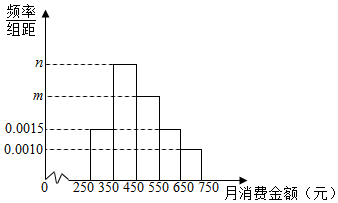

已知[350，450），[450，550），[550，650）三个金额段的学生人数成等差数列，将月消费金额不低于550元的学生称为“高消费群”．
（Ⅰ）求m，n的值，并求这100名学生月消费金额的样本平均数$\overline x$（同一组中的数据用该组区间的中点值作代表）；
（Ⅱ）现采用分层抽样的方式从月消费金额落在[350，450），[550，650）内的两组学生中抽取10人，再从这10人中随机抽取3人，记被抽取的3名学生中属于“高消费群”的学生人数为随机变量X，求X的分布列及数学期望．

Answer 1

分析 （Ⅰ）由题意知 100（m+n）=0.6且2m=n+0.0015，由此能求出m，n的值，并求这100名学生月消费金额的样本平均数$\overline x$．
（Ⅱ）由题意从[350，450）中抽取7人，从[550，650）中抽取3人，随机变量X的取值所有可能取值有0，1，2，3，分别求出相应的概率，由此能求出随机变量X的分布列及随机变量X的数学期望E（X）．

解答 解：（Ⅰ）由题意知 100（m+n）=0.6且2m=n+0.0015，
故m=0.0025，n=0.0035．…（3分）
所求平均数为：$\overline x=300×0.15+400×0.35+500×0.25+600×0.15+700×0.10=470$（元）…（5分）
（Ⅱ）由题意从[350，450）中抽取7人，从[550，650）中抽取3人…（7分）
随机变量X的取值所有可能取值有0，1，2，3，
$P（X=k）=\frac{{C_3^kC_7^{3-k}}}{{C_{10}^3}}（k=0，1，2，3）$…（9分）
所以，随机变量X的分布列为

X	0	1	2	3
P	$\frac{35}{120}$	$\frac{63}{120}$	$\frac{21}{120}$	$\frac{1}{120}$

随机变量X的数学期望E（X）=$0×\frac{35}{120}+1×\frac{63}{120}+2×\frac{21}{120}+3×\frac{1}{120}=\frac{9}{10}$…（12分）

点评 本题考查频率分布直方图的应用，考查离散型随机变量的分布列和数学期望的求法，是中档题，解题时要认真审题，注意排列组合知识的合理运用．