题目内容
已知x∈(- ,0),sinx=-
,0),sinx=- ,则tan2x=
,则tan2x=
- A.-
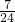
- B.
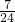
- C.-

- D.

C
分析:角三角函数的基本关系 求出 cosx、tanx,再利用二倍角的正切公式求出tan2x 的值.
解答:∵x∈(- ,0),sinx=-
,0),sinx=- ,∴cosx=
,∴cosx= ,∴tanx=
,∴tanx=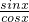 =-
=- ,
,
∴tan2x= =
= =-
=- ,
,
故选C.
点评:本题考查同角三角函数的基本关系,以及二倍角的正切公式的应用,求出cosx值是解题的关键.
分析:角三角函数的基本关系 求出 cosx、tanx,再利用二倍角的正切公式求出tan2x 的值.
解答:∵x∈(-
 ,0),sinx=-
,0),sinx=- ,∴cosx=
,∴cosx= ,∴tanx=
,∴tanx=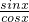 =-
=- ,
,∴tan2x=
 =
= =-
=- ,
,故选C.
点评:本题考查同角三角函数的基本关系,以及二倍角的正切公式的应用,求出cosx值是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知x∈(-
,0),cosx=
,则tan2x=( )
| π |
| 2 |
| 4 |
| 5 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|