题目内容
15.函数$y=cosx,(-\frac{π}{3}<x≤\frac{5π}{6})$的值域为$[-\frac{\sqrt{3}}{2},1]$.分析 先画出余弦函数的图象,由x的范围和图象求出y=cosx的最大值、最小值,可得答案.
解答 解:如右图余弦函数的图象:
∵$-\frac{π}{3}<x≤\frac{5π}{6}$,
∴由图得,当x=0时,y=cosx取最大值是1,
当x=$\frac{5π}{6}$时,y=cosx取最小值是$-\frac{\sqrt{3}}{2}$,
∴函数y=cosx的值域是$[-\frac{\sqrt{3}}{2},1]$,
故答案为:$[-\frac{\sqrt{3}}{2},1]$.
点评 本题考查余弦函数的图象与最值的应用,以及数形结合思想.

练习册系列答案
相关题目
6.双曲线 $\frac{x^2}{{1+{k^2}}}-\frac{y^2}{{8-{k^2}}}=1$(k为常数)的焦点坐标是( )
| A. | (0,±3) | B. | (±3,0) | C. | (±1,0) | D. | (0,±1) |
13.设Sn为等差数列{an}的前n项和,a1=-2,S3=0,则{an}的公差为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
14.设$a={({\frac{1}{2}})^{\frac{1}{2}}},b={({\frac{1}{2}})^{\frac{1}{3}}},c={log_{\frac{1}{2}}}2$,则( )
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
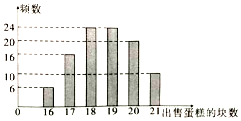 某蛋糕店出售一种蛋糕,这种蛋糕的保质期很短,必须当天卖掉,否则容易变质,该蛋糕店每天以每块16元的成本价格制作这种蛋糕若干块,然后以每块26元的价格出售,如果当天卖不完,剩下的蛋糕只能以每块6元低价出售.蛋糕店记录了100天该种蛋糕的日需求量n(单位:块,n∈N*)整理得如图:
某蛋糕店出售一种蛋糕,这种蛋糕的保质期很短,必须当天卖掉,否则容易变质,该蛋糕店每天以每块16元的成本价格制作这种蛋糕若干块,然后以每块26元的价格出售,如果当天卖不完,剩下的蛋糕只能以每块6元低价出售.蛋糕店记录了100天该种蛋糕的日需求量n(单位:块,n∈N*)整理得如图: