题目内容
(本题满分13分)已知椭圆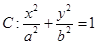 的左焦点
的左焦点 的坐标为
的坐标为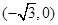 ,
, 是它的右焦点,点
是它的右焦点,点 是椭圆
是椭圆 上一点,
上一点,  的周长等于
的周长等于 .
.
(1)求椭圆 的方程;
的方程;
(2)过定点 作直线
作直线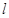 与椭圆
与椭圆 交于不同的两点
交于不同的两点 ,且
,且 (其中
(其中 为坐标原点),求直线
为坐标原点),求直线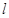 的方程.
的方程.
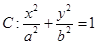 的左焦点
的左焦点 的坐标为
的坐标为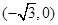 ,
, 是它的右焦点,点
是它的右焦点,点 是椭圆
是椭圆 上一点,
上一点,  的周长等于
的周长等于 .
.(1)求椭圆
 的方程;
的方程;(2)过定点
 作直线
作直线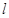 与椭圆
与椭圆 交于不同的两点
交于不同的两点 ,且
,且 (其中
(其中 为坐标原点),求直线
为坐标原点),求直线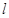 的方程.
的方程.(1)  (2)
(2)  和
和
 (2)
(2)  和
和
试题分析:(1)由已知得
 所以椭圆
所以椭圆 的方程为
的方程为 . (5分)
. (5分) (2)显然直线
 不符合条件,故设直线
不符合条件,故设直线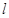 的方程为
的方程为 (6分)
(6分)由

 ……(*) (8分)
……(*) (8分)由

 (10分)
(10分)将(*)式代入得
 解得
解得
当
 时,
时, 
故所求直线
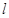 有两条,其方程为
有两条,其方程为 和
和 (13分)
(13分)点评:解决该试题的关键是熟练的运用其性质得到其方程,并结合设而不求的思想来结合韦达定理得到系数与根的关系,进而得到求解,属于中档题。

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
 ,
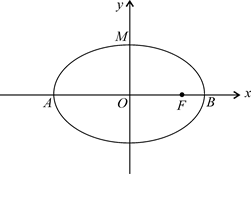
, 为椭圆中心,
为椭圆中心,
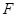 为椭圆的右焦点,
为椭圆的右焦点,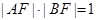 ,
,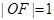 .
.
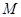 ,直线
,直线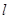 交椭圆于
交椭圆于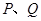 两点,问:是否存在直线
两点,问:是否存在直线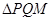 的垂心?若存在,求出直线
的垂心?若存在,求出直线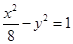 的右焦点为圆心,并与其渐近线相切的圆的标准方程是______
的右焦点为圆心,并与其渐近线相切的圆的标准方程是______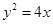 上一点
上一点 到焦点的距离为3,则点
到焦点的距离为3,则点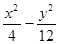 =1的焦点到渐近线的距离为( )。
=1的焦点到渐近线的距离为( )。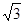
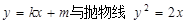 交于A,B两点,且
交于A,B两点,且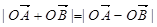 (其中O为坐标原点),若OM⊥AB于M,则点M的轨迹方程为 ( )
(其中O为坐标原点),若OM⊥AB于M,则点M的轨迹方程为 ( )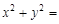 2
2 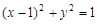
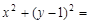 1
1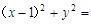 4
4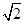 ,离心率e=
,离心率e=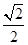 ,过右焦点F的直线l交椭圆于P、Q两点.
,过右焦点F的直线l交椭圆于P、Q两点.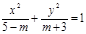 是椭圆”
是椭圆”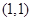 和直线
和直线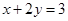 距离相等的点的轨迹是直线
距离相等的点的轨迹是直线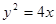 的焦点为F,过抛物线在第一象限部分上一点P的切线为
的焦点为F,过抛物线在第一象限部分上一点P的切线为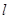 ,过P点作平行于
,过P点作平行于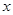 轴的直线
轴的直线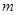 ,过焦点F作平行于
,过焦点F作平行于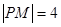 ,则点P的坐标为 。
,则点P的坐标为 。