题目内容
已知直线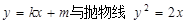 交于A,B两点,且
交于A,B两点,且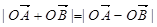 (其中O为坐标原点),若OM⊥AB于M,则点M的轨迹方程为 ( )
(其中O为坐标原点),若OM⊥AB于M,则点M的轨迹方程为 ( )
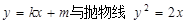 交于A,B两点,且
交于A,B两点,且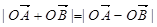 (其中O为坐标原点),若OM⊥AB于M,则点M的轨迹方程为 ( )
(其中O为坐标原点),若OM⊥AB于M,则点M的轨迹方程为 ( )A.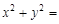 2 2 | B.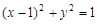 |
C.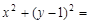 1 1 | D.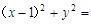 4 4 |
B
试题分析:联立直线方程与抛物线方程并整理得
 ,
,设
 则
则
因为
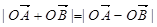 ,所以
,所以 ,所以
,所以 ,代入数据可得
,代入数据可得 ,所以直线
,所以直线 ,所以直线恒过定点(2,0),
,所以直线恒过定点(2,0),因为OM⊥AB,所以
 ,整理得
,整理得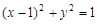 即为点M的轨迹方程.
即为点M的轨迹方程.点评:解决本小题的关键是根据
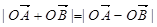 可得
可得 ,从而利用韦达定理知道
,从而利用韦达定理知道 ,本小题运算量比较大,要仔细运算,另外要注意直线过定点问题.
,本小题运算量比较大,要仔细运算,另外要注意直线过定点问题.
练习册系列答案
相关题目
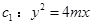 (
(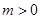 )的准线与
)的准线与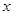 轴交于
轴交于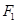 ,焦点为
,焦点为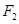 ;以
;以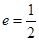 的椭圆
的椭圆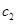 与抛物线
与抛物线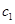 在
在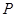 .
.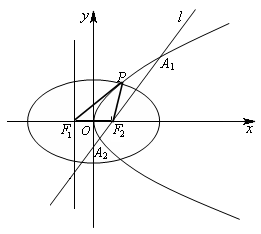
 时,求椭圆的方程;
时,求椭圆的方程; 经过椭圆
经过椭圆 、
、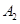 ,如果以线段
,如果以线段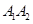 为直径作圆,试判断点
为直径作圆,试判断点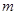 ,使得
,使得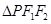 的边长是连续的自然数,若存在,求出这样的实数
的边长是连续的自然数,若存在,求出这样的实数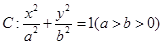 的离心率为
的离心率为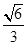 ,焦点到相应准线的距离为
,焦点到相应准线的距离为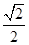
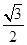 ,求
,求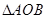 面积的最大值。
面积的最大值。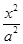 -
- =1的右焦点为
=1的右焦点为 ,则该双曲线的离心率等于( )
,则该双曲线的离心率等于( ) B.
B. C.
C. D.
D.
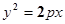 与直线
与直线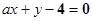 交于A,B两点,其中A点的坐标是
交于A,B两点,其中A点的坐标是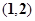 .该抛物线的焦点为F,则
.该抛物线的焦点为F,则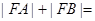 ( )
( )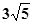
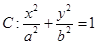 的左焦点
的左焦点 的坐标为
的坐标为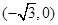 ,
, 是它的右焦点,点
是它的右焦点,点 是椭圆
是椭圆 上一点,
上一点,  的周长等于
的周长等于 .
. 作直线
作直线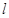 与椭圆
与椭圆 ,且
,且 (其中
(其中 为坐标原点),求直线
为坐标原点),求直线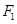 、
、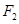 是椭圆
是椭圆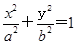 (a>b>0)的两个焦点,以线段
(a>b>0)的两个焦点,以线段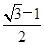
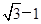
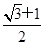

 上,点Q在曲线C2:(x-2)2+y2=1上,点O为坐标原点,则
上,点Q在曲线C2:(x-2)2+y2=1上,点O为坐标原点,则 的最大值是 .
的最大值是 .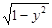 恰有一个公共点,则k的取值范围是___________
恰有一个公共点,则k的取值范围是___________