Question

【题目】定义：过椭圆上的一点（不与长轴的端点重合）与椭圆的两个焦点确定的三角形称为椭圆的焦点三角形；已知过椭圆上一点P（不与长轴的端点重合）的焦点三角形，且．

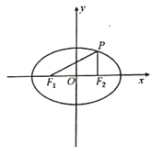
（1）求证：焦点三角形的面积为定值；

（2）已知椭圆的一个焦点三角形为，；

①若，求点的横坐标的范围；

②若，过点的直线与轴交于点，且，记，求的值．

Answer 1

【答案】（1）证明见解析；（2）①或；②或．

【解析】

（1）根据椭圆定义、余弦定理及三角形面积公式推理运算即可；

（2）①先设出点坐标，根据焦半径公式表示出，根据余弦定理用点的横坐标表示出来，再利用的范围求出点的横坐标范围；②利用（1）的结论及条件先求出点坐标，然后在中利用面积公式求出即可.

解：（1）证明：设，由椭圆定义有，在三角形中，由余弦定理得：，

即，所以 .

（2）①设，由已知得：，.

在三角形中，由焦半径公式得：，

由余弦定理得：，

代入并化简得：，故或 .

②由（1）可知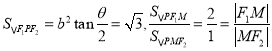，可得，或.

（ⅰ）当时，设，

在三角形中，，

由余弦定理得：得.

则，所以，所以，∴，所以 .

（ⅱ）当时，同理可得

综上所述，或．