题目内容
【题目】在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中选择两个,补充在下面问题中,并给出解答.已知数列
这三个条件中选择两个,补充在下面问题中,并给出解答.已知数列![]() 的前
的前![]() 项和为
项和为![]() ,满足________,________;又知正项等差数列
,满足________,________;又知正项等差数列![]() 满足
满足![]() ,且
,且![]() ,
,![]() ,
,![]() 成等比数列.
成等比数列.
(1)求![]() 和
和![]() 的通项公式;
的通项公式;
(2)证明:![]() .
.
【答案】(1)选法见解析,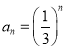 ,
,![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)若选择①②
先由![]() ,当
,当![]() ≥2时,
≥2时,![]() ,两式相减整理得
,两式相减整理得![]() ,再求出
,再求出![]() ,进而说明数列
,进而说明数列![]() 是等比数列,求出
是等比数列,求出![]() ,设正项等差数列
,设正项等差数列![]() 的公差为
的公差为![]() ,由已知条件求出
,由已知条件求出![]() ,进而求得
,进而求得![]() ;
;
若选择②③
先由![]() ,当
,当![]() ≥2时,
≥2时,![]() ,两式相减整理得
,两式相减整理得![]() ,再求出
,再求出![]() ,进而说明数列
,进而说明数列![]() 是等比数列,求出
是等比数列,求出![]() ,设正项等差数列
,设正项等差数列![]() 的公差为
的公差为![]() ,由已知条件求出
,由已知条件求出![]() ,进而求得
,进而求得![]() ;
;
(2)由(1)求得![]() ,再求
,再求![]() ,即可证明结论.
,即可证明结论.
(1)解法一:选择①②
当![]() 时,由
时,由![]() 得
得
![]() ,
,
两式相减,得![]() ,即
,即![]() ,
,
由①得![]() ,即
,即![]() ,
,
∴![]() ,得
,得![]() ,
,
∴![]() ,∴
,∴![]() 为
为![]() ,公比为
,公比为![]() 的等比数列,
的等比数列,
∴![]() .
.
设等差数列![]() 的公差为
的公差为![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() 成等比数列.
成等比数列.
![]() ,即
,即![]() ,
,
解得![]() ,
,![]() (舍去),∴
(舍去),∴![]()
解法二:选择②③
当![]() 时,由③
时,由③![]() ,
,
得![]() ,
,
两式相减,得![]() ,∴
,∴![]() ,
,
又![]() ,得
,得![]() ,
,
∴![]() ,∴
,∴![]() 为
为![]() ,公比为
,公比为![]() 的等比数列,
的等比数列,
∴![]() .
.
(以下同法一)
(2)证明:由(1)得![]()
则![]()
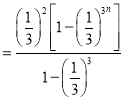
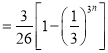
![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目