题目内容
11.定长为l($l>\frac{{2{b^2}}}{a}$)的线段AB的两个端点都在双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的右支上,则AB中点M的横坐标的最小值为( )| A. | $\frac{a(2a+l)}{{2\sqrt{{a^2}+{b^2}}}}$ | B. | $\frac{a+l}{{2\sqrt{{a^2}+{b^2}}}}$ | C. | $\frac{a(l-2a)}{{2\sqrt{{a^2}+{b^2}}}}$ | D. | $\frac{al}{{2\sqrt{{a^2}+{b^2}}}}$ |
分析 用A、B 两点的坐标表示出|FA|和|FB|,解出A、B 两点的坐标,利用|FA|+|FB|≥|AB|,求得m的最小值.
解答 解:设AB中点M的横坐标为m,右焦点为F,离心率为e,AB的中点横坐标为m,
则m=$\frac{1}{2}$(xA+xB),
|FA|=e(xA-$\frac{{a}^{2}}{c}$),|FB|=e(xB-$\frac{{a}^{2}}{c}$),
∴m=$\frac{1}{2}$•$\frac{1}{e}$(|FA|+|FB|)+$\frac{{a}^{2}}{c}$≥$\frac{1}{2e}$|AB|+$\frac{{a}^{2}}{c}$=$\frac{1}{2e}$+$\frac{{a}^{2}}{c}$=$\frac{la}{2c}$+$\frac{{a}^{2}}{c}$
=$\frac{a(2a+l)}{2\sqrt{{a}^{2}+{b}^{2}}}$,
当且仅当F、A、B共线时,m取得最小值.
故选:A.
点评 本题考查双曲线的定义和双曲线的标准方程、以及双曲线的简单性质的应用,注意运用双曲线的第二定义,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.设函数g(x)=x(x2-1),则g(x)在区间[0,1]上的最大值为( )
| A. | -1 | B. | 0 | C. | -$\frac{2\sqrt{3}}{9}$ | D. | $\frac{\sqrt{3}}{3}$ |
2.5名学生站成一排照相,甲、乙之间必须间隔一人的排法共( )
| A. | 12种 | B. | 18种 | C. | 24种 | D. | 36种 |
19.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{4}$=1(a>0)的一个焦点坐标为(2$\sqrt{3}$,0)则实数a的值为( )
| A. | 8 | B. | 2$\sqrt{2}$ | C. | 16 | D. | 4 |
16.若实数x,y满足$\left\{\begin{array}{l}{x-y+1≤0}\\{x>0}\\{y≤2}\end{array}\right.$,则$\frac{2y}{2x+1}$的取值范围是( )
| A. | [$\frac{4}{3}$,4] | B. | [$\frac{4}{3}$,4) | C. | [2,4] | D. | (2,4] |
20.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体最长的棱长为( )
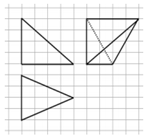

| A. | $4\sqrt{3}$ | B. | $4\sqrt{2}$ | C. | 6 | D. | $2\sqrt{5}$ |
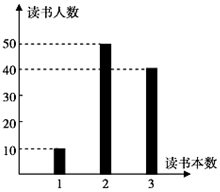 某校开展“读好书,好读书”活动,要求本学期每人至少读一本课外书,该校高一共有100名学生,他们本学期读课外书的本数统计如图所示.
某校开展“读好书,好读书”活动,要求本学期每人至少读一本课外书,该校高一共有100名学生,他们本学期读课外书的本数统计如图所示.