题目内容
19.已知平面ABCD⊥平面ADEF,AB⊥AD,CD⊥AD,且AB=1,AD=CD=2,ADEF是正方形,在正方形ADEF内部有一点M,满足MB、MC与平面ADEF所成的角相等,则点M的轨迹长度为( )| A. | $\frac{4}{3}$ | B. | $\frac{16}{3}$ | C. | $\frac{4}{9}π$ | D. | $\frac{8}{3}$π |
分析 建立空间直角坐标,求得B,C和M点坐标,由题意可知2丨MB丨=丨MC丨,利用空间中两点之间的距离公式,即可求得M的轨迹方程,即可求得点M的轨迹长度.
解答 解:由题意可知,以D为原点,分别以DA,DC,DE为x,y,z轴,建立空间直角坐标系,
则B(2,1,0),C(0,2,0),M(x,0,z),
由直线MB,MC与平面ADEF所成的角,∠AMB,∠DMC,均为锐角,
∴sin∠AMB=sin∠DMC,即$\frac{丨AB丨}{丨MB丨}$=$\frac{丨CD丨}{丨MC丨}$,即2丨MB丨=丨MC丨,
则2$\sqrt{(2-x)^{2}+{1}^{2}+{z}^{2}}$=$\sqrt{{x}^{2}+{2}^{2}+{z}^{2}}$,整理得:(x-$\frac{8}{3}$)2+z2=$\frac{16}{9}$,
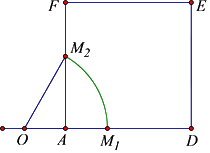
由此可得:M在正方形ADEF内的轨迹是以点O($\frac{8}{3}$,0,0)为圆心,以$\frac{4}{3}$为半径的圆弧M1M2,
则圆心角∠M1OM2=$\frac{π}{3}$,
则圆弧M1M2弧长l,l=$\frac{π}{3}$×$\frac{4}{3}$=$\frac{4π}{9}$,
故选C.
点评 本题考查空间向量的坐标表示,考查空间中两点之间的距离公式,轨迹方程的求法,考查数形结合思想,属于中档题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
10.下列四个函数中,以π为最小正周期,且在区间$(\frac{π}{2},π)$上为增函数的是( )
| A. | y=sin2x | B. | y=|cosx| | C. | y=-tanx | D. | $y=cos\frac{x}{2}$ |
14.已知双曲线C:$\frac{{x}^{2}}{m}$-$\frac{{y}^{2}}{6}$=1(m>0)的右焦点为F,则点F到渐近线的距离为( )
| A. | $\sqrt{6}$ | B. | 6 | C. | $\sqrt{3}$ | D. | 3 |
9.设集合A={x|x2-4x+3<0},B={x|log2x>1},则A∩B=( )
| A. | (-1,3) | B. | (-1,2) | C. | (1,3) | D. | (2,3) |
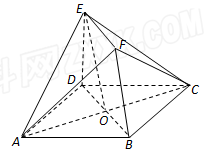 如图,正方形ABCD和直角梯形BDEF所在的平面互相垂直,O为正方形ABCD的中心,AD=DE=2$\sqrt{2}$,EF∥BD,BD=2EF,DE⊥BD.
如图,正方形ABCD和直角梯形BDEF所在的平面互相垂直,O为正方形ABCD的中心,AD=DE=2$\sqrt{2}$,EF∥BD,BD=2EF,DE⊥BD.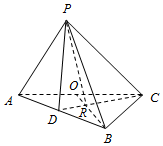 在三棱锥P-ABC中,AB⊥BC,AB=6,$BC=2\sqrt{3}$,O为AC的中点,过C作BO的垂线,交BO、AB分别于R、D.若∠DPR=∠CPR,则三棱锥P-ABC体积的最大值为3$\sqrt{3}$.
在三棱锥P-ABC中,AB⊥BC,AB=6,$BC=2\sqrt{3}$,O为AC的中点,过C作BO的垂线,交BO、AB分别于R、D.若∠DPR=∠CPR,则三棱锥P-ABC体积的最大值为3$\sqrt{3}$.