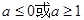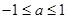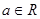题目内容
求形如 的函数的导数,我们常采用以下做法:先两边同取自然对数得:
的函数的导数,我们常采用以下做法:先两边同取自然对数得: ,再两边同时求导得
,再两边同时求导得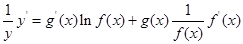 ,于是得到:
,于是得到: ,运用此方法求得函数
,运用此方法求得函数 的一个单调递增区间是( )
的一个单调递增区间是( )
A. | B. | C. | D. |
C
解析试题分析:两边同取自然对数得: ,再两边同时求导得
,再两边同时求导得 ,得
,得 ,由
,由 得
得 解得
解得 .
.
考点:1.新定义题;2.导数运算.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)的定义域为R,对任意 ,有
,有 ,且
,且 ,则f(x)<3x+6的解集为( )
,则f(x)<3x+6的解集为( )
| A.(-1, 1) | B.(-1,+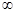 ) ) | C.(-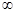 ,-1) ,-1) | D.(-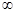 ,+ ,+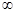 ) ) |
已知函数f(x)(x∈R)满足 >f(x),则 ( )
>f(x),则 ( )
A.f(2)< f(0) f(0) | B.f(2)≤ f(0) f(0) |
C.f(2)= f(0) f(0) | D.f(2)> f(0) f(0) |
设 ,若f(3)="3f" ′(x0),则x0=( )
,若f(3)="3f" ′(x0),则x0=( )
| A.±1 | B.±2 | C.± | D.2 |
已知函数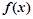 定义在R上的奇函数,当
定义在R上的奇函数,当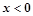 时,
时,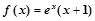 ,给出下列命题:
,给出下列命题:
①当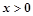 时,
时, ②函数
②函数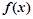 有2个零点
有2个零点
③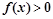 的解集为
的解集为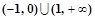 ④
④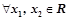 ,都有
,都有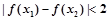
其中正确命题个数是( )
| A.1 | B.2 | C.3 | D.4 |
函数 为自然对数的底数)的值域是实数集R,则实数a的取值范围是( )
为自然对数的底数)的值域是实数集R,则实数a的取值范围是( )
A. | B. | C. | D.[0,1] |
设直线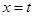 与函数
与函数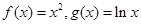 的图象分别交于点
的图象分别交于点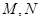 ,则当
,则当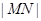 达到最小时
达到最小时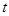 的值为( )
的值为( )
| A.1 | B.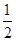 | C.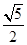 | D.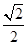 |
对于实数集 上的可导函数
上的可导函数 ,若满足
,若满足 ,则在区间[1,2]上必有( )
,则在区间[1,2]上必有( )
A. |
B. |
C. |
D. 或 或 |
 满足:①当
满足:①当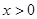 时,
时, 恒成立;②对任意的
恒成立;②对任意的 都有
都有 。又函数
。又函数 满足:对任意的
满足:对任意的 成立,当
成立,当 时,
时, 。若关于
。若关于 的不等式
的不等式 对
对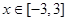 恒成立,则
恒成立,则 的取值范围( )
的取值范围( )