题目内容
(本题满分12分)
如图,已知椭圆的中心在坐标原点,焦点在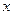 轴上,它的一个顶点为
轴上,它的一个顶点为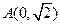 ,且离心率等于
,且离心率等于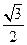 ,过点
,过点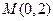 的直线
的直线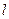 与椭圆相交于不同两点
与椭圆相交于不同两点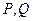 ,点
,点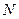 在线段
在线段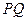 上。
上。

(1)求椭圆的标准方程;
(2)设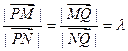 ,若直线
,若直线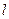 与
与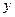 轴不重合,
轴不重合,
试求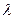 的取值范围。
的取值范围。
如图,已知椭圆的中心在坐标原点,焦点在
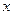 轴上,它的一个顶点为
轴上,它的一个顶点为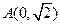 ,且离心率等于
,且离心率等于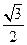 ,过点
,过点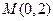 的直线
的直线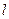 与椭圆相交于不同两点
与椭圆相交于不同两点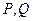 ,点
,点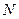 在线段
在线段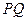 上。
上。
(1)求椭圆的标准方程;
(2)设
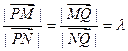 ,若直线
,若直线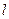 与
与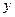 轴不重合,
轴不重合,试求
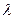 的取值范围。
的取值范围。.解(1)设椭圆的标准方程是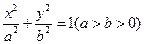 。
。
由于椭圆的一个顶点是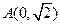 ,故
,故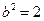 ,根据离心率是
,根据离心率是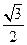 得,
得,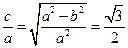 ,解得
,解得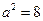 。
。
所以椭圆的标准方程是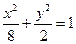 。 ........... (4分)
。 ........... (4分)
(2)设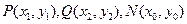 。
。
设直线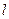 的方程为
的方程为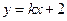 ,与椭圆方程联立消去
,与椭圆方程联立消去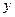 得
得
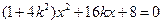 ,根据韦达定理得
,根据韦达定理得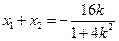 ,
,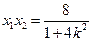 8分
8分
由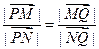 ,得
,得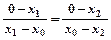 ,整理得
,整理得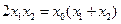 ,
,
把上面的等式代入得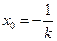 ,又点
,又点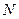 在直线
在直线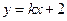 上,所以
上,所以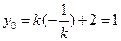 ,
,
于是有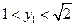 .....(10分)
.....(10分)
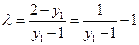 ,由
,由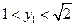 ,得
,得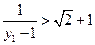 ,
,
∴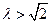 .综上所述
.综上所述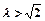 。。,....(12分)
。。,....(12分)
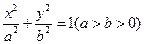 。
。由于椭圆的一个顶点是
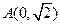 ,故
,故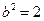 ,根据离心率是
,根据离心率是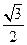 得,
得,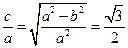 ,解得
,解得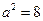 。
。所以椭圆的标准方程是
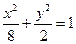 。 ........... (4分)
。 ........... (4分)(2)设
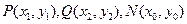 。
。设直线
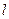 的方程为
的方程为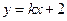 ,与椭圆方程联立消去
,与椭圆方程联立消去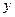 得
得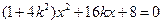 ,根据韦达定理得
,根据韦达定理得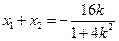 ,
,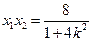 8分
8分由
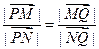 ,得
,得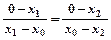 ,整理得
,整理得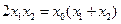 ,
,把上面的等式代入得
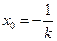 ,又点
,又点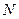 在直线
在直线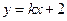 上,所以
上,所以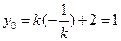 ,
,于是有
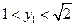 .....(10分)
.....(10分)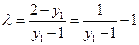 ,由
,由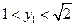 ,得
,得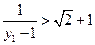 ,
,∴
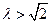 .综上所述
.综上所述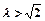 。。,....(12分)
。。,....(12分)略

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
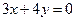 ,且过点
,且过点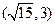 的双曲线的标准方程,并求此双曲线的离心率.
的双曲线的标准方程,并求此双曲线的离心率.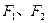 为椭圆
为椭圆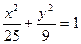 的两个焦点,过
的两个焦点,过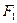 的直线交椭圆于A、B两点若
的直线交椭圆于A、B两点若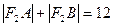 ,则
,则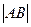 =______
=______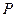 是以
是以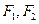 为焦点的椭圆
为焦点的椭圆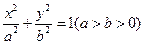 上一点,且
上一点,且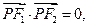
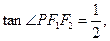 则该椭圆的离心率等于_______
则该椭圆的离心率等于_______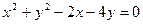 截直线
截直线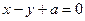 得弦长为
得弦长为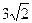 ,则a的值为(
,则a的值为(  )
)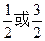
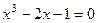 时,若初始区间为
时,若初始区间为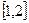 ,则下一个有解的区间是
,则下一个有解的区间是 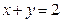
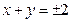
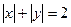
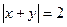
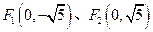 ,动点
,动点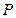 满足条件:
满足条件: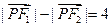 ,设点
,设点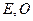 为坐标原点。
为坐标原点。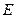 的方程;
的方程;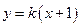 与曲线
与曲线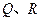 ,求
,求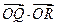 的取值范围;
的取值范围;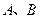 两点分别在直线
两点分别在直线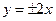 上,若
上,若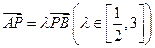 ,记
,记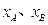 分别为
分别为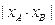 的最小值。
的最小值。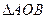 面积的最大值。
面积的最大值。