题目内容
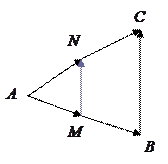
已知A、B、C是直线l上的不同三点,O是l外一点,向量
,
,
满足
=(
x2+1)
-(lnx-y)
,记y=f(x);
(1)求函数y=f(x)的解析式;
(2)求函数y=f(x)的单调区间.
| OA |
| OB |
| OC |
| OA |
| 3 |
| 2 |
| OB |
| OC |
(1)求函数y=f(x)的解析式;
(2)求函数y=f(x)的单调区间.
(1)∵
=(
x2+1)
-(lnx-y)
,且A、B、C是直线l上的不同三点,
∴(
x2+1)-(lnx-y)=1,∴y=
x2-lnx;(6分)
(2)∵f(x)=
x2-lnx,
∴f′(x)=3x-
=
,(8分)
∵f(x)=
x2-lnx的定义域为(0,+∞),而f′(x)=
>0,可得x>
∴y=f(x)在(
,+∞)上为增函数,在(0,
)是减函数,即y=f(x)的单调增区间为(0,+∞),单调递减区间是(0,
).(12分)
| OA |
| 3 |
| 2 |
| OB |
| OC |
∴(
| 3 |
| 2 |
| 3 |
| 2 |
(2)∵f(x)=
| 3 |
| 2 |
∴f′(x)=3x-
| 1 |
| x |
| 3x2-1 |
| x |
∵f(x)=
| 3 |
| 2 |
| 3x2-1 |
| x |
| ||
| 3 |
∴y=f(x)在(
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |

练习册系列答案
相关题目
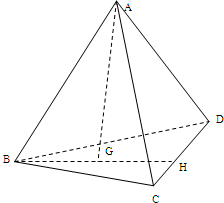
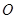 为极点,
为极点,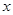 轴的正半轴为极轴,已知点
轴的正半轴为极轴,已知点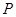 的直角坐标为
的直角坐标为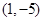 ,点
,点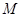 的极坐标为
的极坐标为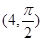 ,若直线
,若直线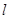 过点
过点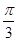 ,圆
,圆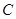 以
以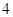 为半径。
为半径。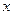 轴上,它的一个顶点为
轴上,它的一个顶点为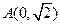 ,且离心率等于
,且离心率等于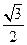 ,过点
,过点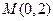 的直线
的直线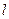 与椭圆相交于不同两点
与椭圆相交于不同两点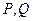 ,点
,点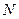 在线段
在线段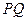 上。
上。
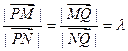 ,若直线
,若直线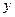 轴不重合,
轴不重合,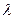 的取值范围。
的取值范围。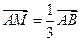 ,
,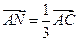 .求证:
.求证: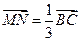 .
.