题目内容
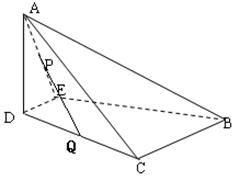
如图,沿等腰直角三角形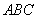 的中位线
的中位线 ,将平面
,将平面 折起,使得平面
折起,使得平面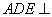 平面
平面 得到四棱锥
得到四棱锥 .
.
(1)求证:平面 平面
平面 ;
;
(2)过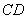 的中点
的中点 的平面
的平面 与平面
与平面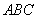 平行,试求平面
平行,试求平面 与四棱锥
与四棱锥 各个面的交线所围成多边形的面积与三角形
各个面的交线所围成多边形的面积与三角形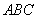 的面积之比。
的面积之比。

【答案】
【解析】(1) ,平面
,平面 平面
平面 ,根据两个平面垂直的性质定理得
,根据两个平面垂直的性质定理得 平面
平面 ,所以
,所以 ,又
,又 ,根据线面垂直的判定定理
,根据线面垂直的判定定理 平面
平面 ,
, 平面
平面 ,所以平面
,所以平面 平面
平面 。
。
(2)由于平面 平面
平面 ,故平面
,故平面 与平面
与平面 的交线
的交线
 ,
, 是
是 的中点,故
的中点,故 是
是 的中点;同理平面
的中点;同理平面 与平面
与平面 的交线
的交线 ,
, 为
为 的中点;平面
的中点;平面 的交线
的交线 ,
, 为
为 的中点,连接
的中点,连接 即为平面
即为平面 与平面
与平面 的交线,故平面
的交线,故平面 与四棱锥
与四棱锥 各个面的交线所围成多边形是图中的四边形
各个面的交线所围成多边形是图中的四边形 ,由于
,由于 ,故
,故 ,根据(1)
,根据(1) ,由
,由 ,故
,故 ,即四边形
,即四边形 `是直角梯形。
`是直角梯形。
设 ,则
,则 ,故四边形
,故四边形 的面积是
的面积是 ,三角形
,三角形 的面积是
的面积是 ,故平面
,故平面 与四棱锥
与四棱锥 各个面的交线所围成多边形的面积与三角形
各个面的交线所围成多边形的面积与三角形 的面积之比为
的面积之比为 。
。


练习册系列答案
相关题目
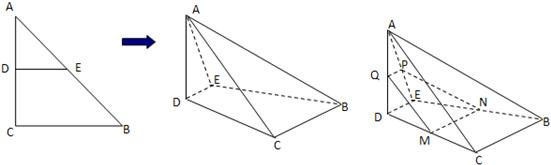
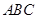 的中位线
的中位线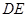 ,将平面
,将平面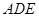 折起,平面
折起,平面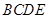 ,得到四棱锥
,得到四棱锥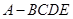 ,
,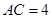 ,设
,设 、
、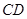 的中点分别为
的中点分别为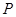 、
、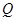 ,
,
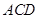

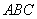 的中位线
的中位线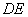 ,将平面
,将平面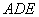 折起,使得平面
折起,使得平面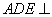 平面
平面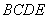 得到四棱锥
得到四棱锥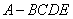 .
.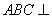 平面
平面 ;
; 的中点
的中点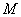 的平面
的平面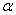 与平面
与平面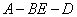 的余弦值。
的余弦值。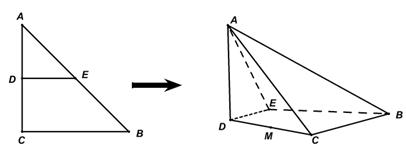


 (3)求异面直线
(3)求异面直线