[题目]设圆的圆心为A.直线过点B(1,0)且与x轴不重合.设P为圆A上一点.线段PB的垂直平分线交直线PA于E(1)证明为定值.并写出E的轨迹方程,(2)设点M的轨迹为曲线C1.直线交C1于M,N两点.问:在轴上是否存在定点D使直线DM与DN的倾斜角互补.若存在求出D点的坐标.否则说明理由. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】设圆的圆心为A，直线过点B（1,0）且与x轴不重合，设P为圆A上一点，线段PB的垂直平分线交直线PA于E

（1）证明为定值，并写出E的轨迹方程；

（2）设点M的轨迹为曲线C1，直线交C1于M,N两点，问：在轴上是否存在定点D使直线DM与DN的倾斜角互补，若存在求出D点的坐标，否则说明理由。

【答案】（1）；（2）存在使直线DM与DN的倾斜角互补.

【解析】

(1)由椭圆的定义可判断出点E的轨迹，进而可求出轨迹方程；

(2)先由题意设直线方程为，与椭圆方程联立，由根与系数关系，以及直线DM与DN的倾斜角互补，即可求出结果.

（I）∵E为线段PB的垂直平分线上一点，∴

∴>

∴点E的轨迹是以A,B为焦点的椭圆，2a=4.c=1, ∴

E的轨迹方程。

（II）由于直线过点B（1,0）且与x轴不重合，所以可设方程为

联立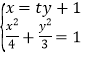消去x得，

设，则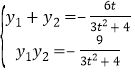

令,若直线DM与DN的倾斜角互补，则

∴ ∴

即∴

∴∴∴

所以存在使直线DM与DN的倾斜角互补.

练习册系列答案

相关题目

【题目】已知指数函数满足．又定义域为实数集R的函数是奇函数．

①确定的解析式；

②求的值；

③若对任意的R，不等式恒成立，求实数的取值范围．

【题目】对于函数，若，则称为的“不动点”；若，则称为的“稳定点”．函数的“不动点”和“稳定点”的集合分别记为和，即，．

（）设函数，求集合和．

（）求证：．

（）设函数，且，求证：．

【题目】以下判断正确的是（）

A. 函数为上的可导函数，则是为函数极值点的充要条件

B. 若命题为假命题，则命题与命题均为假命题

C. 若，则的逆命题为真命题

D. 在中，“”是“”的充要条件

【题目】(本小题满分12分)

已知数列的前项和，且．

（Ⅰ）求数列的通项公式；

（Ⅱ）令，是否存在，使得、、成等比数列．若存在，求出所有符合条件的值；若不存在，请说明理由．

【题目】目前，某市出租车的计价标准是：路程以内（含）按起步价8元收取，超过后的路程按1.9元收取，但超过后的路程需加收的返空费（即单价为元）

（1）若，将乘客搭乘一次出租车的费用（单位：元）表示为行程（单位：）的分段函数；

（2）某乘客行程为，他准备先乘一辆出租车行驶，然后再换乘另一辆出租车完成余下路程，请问：他这样做是否比只乘一辆出租车完成全程更省钱？

【题目】已知等差数列{an}的各项均为正数，其公差为2，a2a4＝4a3＋1.

(1)求{an}的通项公式；

(2)求.

【题目】从原点向圆作两条切线，切点分别为,，记切线，的斜率分别为，．

（Ⅰ）若圆心，求两切线，的方程；

（Ⅱ）若，求圆心的轨迹方程．

【题目】攀枝花是一座资源富集的城市，矿产资源储量巨大，已发现矿种76种，探明储量39种，其中钒、钛资源储量分别占全国的63%和93%，占全球的11%和35%，因此其素有“钒钛之都”的美称．攀枝花市某科研单位在研发钛合金产品的过程中发现了一种新合金材料，由大数据测得该产品的性能指标值（值越大产品的性能越好）与这种新合金材料的含量（单位：克）的关系为：当时，是的二次函数；当时，．测得部分数据如下表：

（单位：克）	0	2	6	10	…
		8	8		…

（Ⅰ）求关于的函数关系式；

（Ⅱ）求该新合金材料的含量为何值时产品的性能达到最佳．

试题分类