题目内容
11.函数f(x)=2sin(ωx+$\frac{π}{4}$)(ω>0)与函数g(x)=cos(2x+φ)(|φ|<$\frac{π}{2}$)的对称轴完全相同,则φ=( )| A. | -$\frac{π}{4}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | -$\frac{π}{2}$ |
分析 由条件利用三角函数的周期性求得ω的值,再根据三角函数的图象的对称性求得φ的值.,
解答 解:∵函数f(x)=2sin(ωx+$\frac{π}{4}$)(ω>0)与函数g(x)=cos(2x+φ)(|φ|<$\frac{π}{2}$)的对称轴完全相同,
故它们的周期相同,即$\frac{2π}{ω}$=$\frac{2π}{2}$,∴ω=2.
故函数f(x)=2sin(2x+$\frac{π}{4}$)(ω>0),函数g(x)=cos(2x+φ)(|φ|<$\frac{π}{2}$).
令2x+$\frac{π}{4}$=kπ+$\frac{π}{2}$,求得x=$\frac{kπ}{2}$+$\frac{π}{8}$,可得f(x)的图象的对称轴为x=$\frac{kπ}{2}$+$\frac{π}{8}$,k∈Z.
令2x+$\frac{φ}{2}$=kπ,求得x=$\frac{kπ}{2}$-$\frac{φ}{2}$,可得f(x)的图象的对称轴为x=$\frac{kπ}{2}$-$\frac{φ}{2}$,k∈Z.
故有-$\frac{φ}{2}$=$\frac{π}{8}$,∴φ=-$\frac{π}{4}$,
故选:A.
点评 本题主要考查三角函数的周期性以及它们的图象的对称性,属于基础题.

练习册系列答案
相关题目
20.已知某程序框图如图所示,则执行该程序后输出的结果是( )


| A. | -1 | B. | -2 | C. | 2 | D. | $\frac{1}{2}$ |
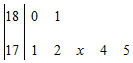 (文科)某校女子篮球队7名运动员身高(单位:厘米)分布的茎叶图如图,已知记录的平均身高为175cm,但记录中有一名运动员身高的末位数字不清晰,如果把其末尾数记为x,那么x的值为2.
(文科)某校女子篮球队7名运动员身高(单位:厘米)分布的茎叶图如图,已知记录的平均身高为175cm,但记录中有一名运动员身高的末位数字不清晰,如果把其末尾数记为x,那么x的值为2.