题目内容
6.设数列{an}的各项均为正数,前n项和Sn满足Sn=$\frac{1}{6}$(an2+3an-4),则an=3n+1.分析 由6Sn=an2+3an-4可推出$6{a_{n+1}}=a_{n+1}^2-a_n^2+3{a_{n+1}}-3{a_n}$,从而可得an+1-an=3,从而求{an}的通项公式.
解答 解:当n=1时,6S1=a12+3a1-4,
即a12-3a1-4=0,得a1=4或a1=-1(舍).
由题意得:6Sn+1=an+12+3an+1-4,…①,
6Sn=an2+3an-4,…②
①-②得:$6{a_{n+1}}=a_{n+1}^2-a_n^2+3{a_{n+1}}-3{a_n}$,
即(an+1+an)(an+1-an-3)=0,
∵an>0,∴an+1-an=3,
∴{an}是以4为首项,3为公差的等差数列,
∴an=4+3(n-1)=3n+1.
故答案为:3n+1.
点评 本题考查数列的通项公式的求法,解题时要认真审题,属于中档题.

练习册系列答案
相关题目
11.函数f(x)=2sin(ωx+$\frac{π}{4}$)(ω>0)与函数g(x)=cos(2x+φ)(|φ|<$\frac{π}{2}$)的对称轴完全相同,则φ=( )
| A. | -$\frac{π}{4}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | -$\frac{π}{2}$ |
15.执行如图的程序框图,输出S的值为( )
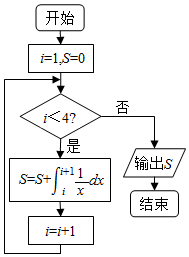

| A. | ln4 | B. | ln5 | C. | ln 5-ln4 | D. | ln 4-ln 3 |
 如图,已知在△ABC中,AC的中点为E,AB的中点为F,延长BE至P,使BE=EP,延长CF至Q,使CF=FQ.试用向量方法证明P,A,Q三点共线.
如图,已知在△ABC中,AC的中点为E,AB的中点为F,延长BE至P,使BE=EP,延长CF至Q,使CF=FQ.试用向量方法证明P,A,Q三点共线.