题目内容
已知等差数列 满足:
满足: ,该数列的前三项分别加上l,l,3后顺次成为等比数列
,该数列的前三项分别加上l,l,3后顺次成为等比数列 的前三项.
的前三项.
(I)求数列 ,
, 的通项公式;
的通项公式;
(II)设 ,若
,若 恒成立,求c的最小值.
恒成立,求c的最小值.
(Ⅰ)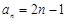 (
(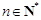 ),
),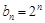 (
(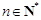 ).
).
(Ⅱ)使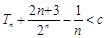
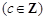 恒成立的
恒成立的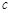 的最小值为
的最小值为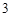 .
.
解析试题分析:(Ⅰ)设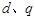 分别为数列
分别为数列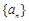 的公差、数列
的公差、数列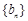 的公比.
的公比.
由题意知,建立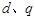 的方程组即得解.
的方程组即得解.
(Ⅱ)利用“错位相减法”求得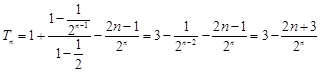 ,
,
利用“放缩法”得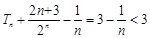 .
.
从而得到使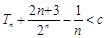
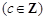 恒成立的
恒成立的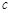 的最小值为
的最小值为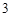 .
.
试题解析:(Ⅰ)设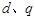 分别为数列
分别为数列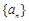 的公差、数列
的公差、数列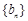 的公比.
的公比.
由题意知,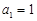 ,
,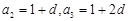 ,分别加上
,分别加上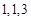 得
得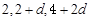 ,
,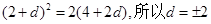
又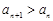 ,所以
,所以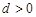 ,所以
,所以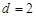 ,
,
所以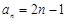 (
(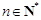 ),
),
由此可得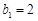
 ,
,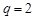 ,所以
,所以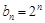 (
(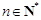 ). 6分
). 6分
(Ⅱ)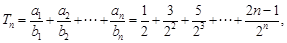 ①
①
∴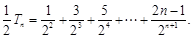 ②
②
由①-②得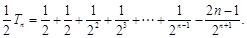
∴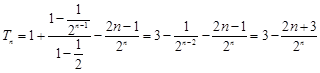 , 10分
, 10分
∴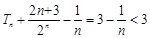 .
.
∴使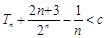
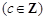 恒成立的
恒成立的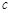 的最小值为
的最小值为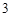 .12分
.12分
考点:等差数列、等比数列,“错位相减法”,“放缩法”.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
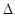 ABC中,三个内角A,B,C的对边分别为
ABC中,三个内角A,B,C的对边分别为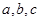 ,且A,B,C成等差数列,
,且A,B,C成等差数列,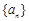 的前n项和为
的前n项和为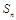 ,且
,且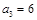 ,
,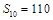 .
. 的通项公式;
的通项公式;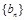 前n项和为
前n项和为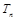 ,且
,且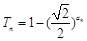 ,令
,令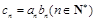 .求数列
.求数列 的前n项和
的前n项和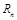 .
.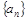 满足:
满足: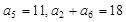 .
.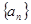 的通项公式;
的通项公式;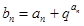 (
(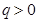 ),求数列
),求数列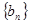 的前n项和
的前n项和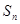 .
. 是等差数列
是等差数列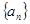 的前
的前 项和,满足
项和,满足 ;
;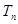 是数列
是数列 的前
的前 .
. 的前
的前 .
.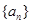 的前
的前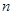 项和为
项和为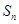 ,且
,且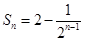 .
.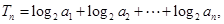 求证:
求证: .
. 为等比数列,
为等比数列,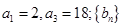 是等差数列,
是等差数列,
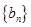 的通项公式及前
的通项公式及前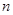 项和
项和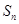 ;
;
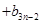 ,
,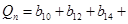
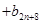 ,其中
,其中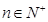 ,试比较
,试比较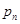 与
与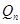 的大小,并加以证明.
的大小,并加以证明.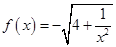 ,数列
,数列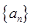 的前
的前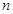 项和为
项和为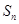 ,点
,点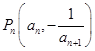 在曲线
在曲线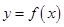 上
上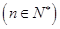 ,且
,且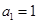 ,
,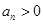 .
.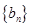 的前
的前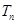 ,且满足
,且满足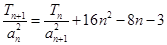 ,
,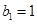 ,求数列
,求数列 ,
,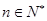 .
.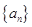 的前
的前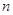 项和为
项和为 ,
,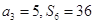 .
. 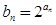 ,求数列
,求数列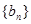 的前
的前 项和
项和 .
.