题目内容
已知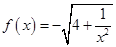 ,数列
,数列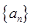 的前
的前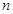 项和为
项和为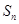 ,点
,点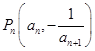 在曲线
在曲线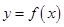 上
上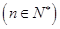 ,且
,且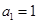 ,
,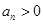 .
.
(1)求数列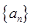 的通项公式;
的通项公式;
(2)数列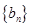 的前
的前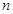 项和为
项和为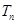 ,且满足
,且满足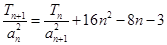 ,
,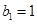 ,求数列
,求数列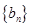 的通项公式;
的通项公式;
(3)求证: ,
,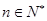 .
.
(1)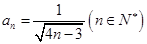 ;(2)
;(2)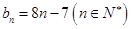 ;(3)详见解析.
;(3)详见解析.
解析试题分析:(1)先根据函数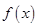 的解析式,由条件“点
的解析式,由条件“点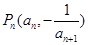 在曲线
在曲线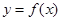 上
上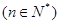 ”上得出
”上得出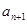 与
与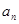 之间的递推关系式,然后进行变形得到
之间的递推关系式,然后进行变形得到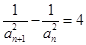 ,于是得到数列
,于是得到数列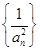 为等差数列,先求出数列
为等差数列,先求出数列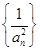 的通项公式,进而求出数列
的通项公式,进而求出数列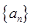 的通项公式;(2)根据(1)中的结果结合已知条件得到
的通项公式;(2)根据(1)中的结果结合已知条件得到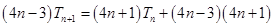 ,两边同时除以
,两边同时除以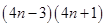 ,得到
,得到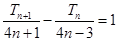 ,构造数列
,构造数列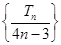 为等差数列,先求出数列
为等差数列,先求出数列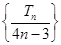 的通项公式,然后求出
的通项公式,然后求出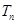 ,然后由
,然后由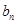 与
与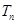 之间的关系求出数列
之间的关系求出数列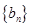 的通项公式;(3)对数列
的通项公式;(3)对数列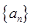 中的项进行放缩法
中的项进行放缩法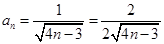
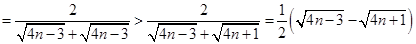 ,再利用累加法即可证明相应的不等式.
,再利用累加法即可证明相应的不等式.
试题解析:(1)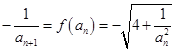 且
且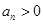 ,∴
,∴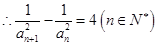 ,
,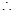 数列
数列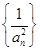 是等差数列,首项
是等差数列,首项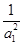 ,公差
,公差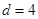 ,
,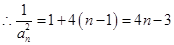 ,
,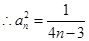 ,
,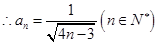 ;
;
(2)由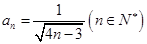 ,
,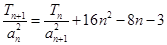 ,
,
得 ,
,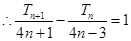 ,
,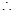 数列
数列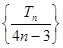 是等差数列,首项为
是等差数列,首项为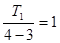 ,公差为
,公差为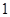 ,
,
∴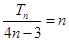 ,
,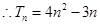 ,当
,当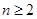 时,
时,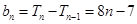 ,
,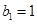 也满足上式,
也满足上式,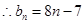 ,
,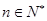 ;
;
(3)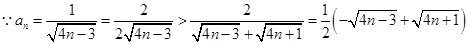 ,
,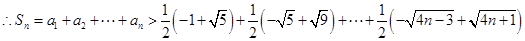
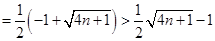 .
.
考点:1.构造等差数列求通项;2.定义法求通项公式;3.放缩法证明数列不等式

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
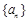 中,前n项和为
中,前n项和为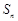 ,且
,且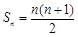 .
.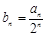 ,数列
,数列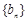 前n项和为
前n项和为 ,求
,求 满足:
满足: ,该数列的前三项分别加上l,l,3后顺次成为等比数列
,该数列的前三项分别加上l,l,3后顺次成为等比数列 的前三项.
的前三项. ,若
,若 恒成立,求c的最小值.
恒成立,求c的最小值.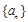 前三项的和为
前三项的和为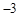 ,前三项的积为
,前三项的积为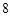 .
.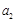 ,
,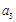 ,
,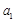 成等比数列,求数列
成等比数列,求数列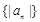 的前
的前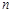 项和.
项和. 是公比大于1的等比数列,
是公比大于1的等比数列, 为数列
为数列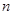 项和.已知
项和.已知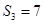 ,且
,且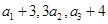 构成等差数列.
构成等差数列.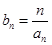 ,求数列
,求数列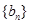 的前
的前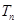 .
. 满足:
满足: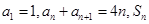 是数列
是数列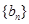 前n项的积为
前n项的积为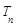 ,且
,且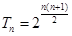
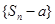 成等差数列?若存在,求出a,若不存在,说明理由;
成等差数列?若存在,求出a,若不存在,说明理由;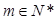 ,满足对任意自然数
,满足对任意自然数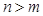 时,
时,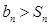 恒成立,若存在,求出m的值;若不存在,说明理由.
恒成立,若存在,求出m的值;若不存在,说明理由. ,公差
,公差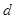 不为零,
不为零,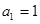 ,且
,且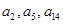 成等比数列;
成等比数列;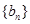 满足
满足 ,求数列
,求数列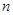 项和
项和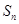 .
.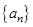 为等差数列,且
为等差数列,且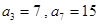 .
.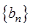 满足
满足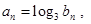 求数列
求数列 项和
项和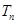 .
.