题目内容
已知 是等差数列
是等差数列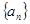 的前
的前 项和,满足
项和,满足 ;
;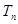 是数列
是数列 的前
的前 项和,满足:
项和,满足: .
.
(1)求数列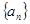 ,
, 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 .
.
(1)数列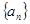 ,
, 的通项公式分别为
的通项公式分别为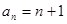 ,
,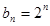 ;(2)
;(2)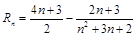 .
.
解析试题分析:(1)由已知条件,首先设;等差数列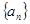 的公差
的公差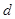 ,列出关于首项和公差
,列出关于首项和公差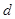 的方程组,解这个方程组,可得
的方程组,解这个方程组,可得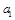 和
和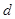 的值,进而可以写出数列
的值,进而可以写出数列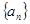 的通项公式.由数列
的通项公式.由数列 的前
的前 项和
项和 ,写出
,写出 ,两式相减并化简整理,得
,两式相减并化简整理,得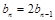 ,从而
,从而 是以2为公比的等比数列,从而可求得数列
是以2为公比的等比数列,从而可求得数列 的通项公式;(2)先写出数列
的通项公式;(2)先写出数列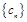 的前
的前 项和
项和 的表达式,分析其结构特征,利用分组求和法及裂项相消法求
的表达式,分析其结构特征,利用分组求和法及裂项相消法求 .
.
试题解析:(1)设等差数列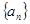 的公差
的公差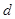 ,则有
,则有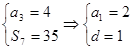 ,所以
,所以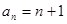 .
.
2分 ,
, ,两式相减得:
,两式相减得: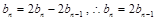 且
且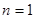 也满足,所以
也满足,所以 是以2为公比的等比数列,又因为
是以2为公比的等比数列,又因为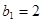 ,所以,
,所以,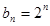 6分
6分
(2)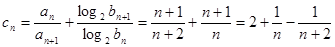 9分
9分
所以: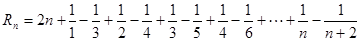
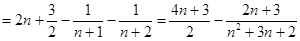 12分
12分
考点:1.等差数列、等比数列的通项公式;2.数列前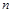 项的和.
项的和.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
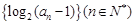 为等差数列,且
为等差数列,且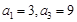 .
.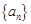 的通项公式;
的通项公式;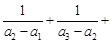 …
…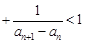 .
.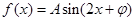
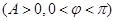 ,当
,当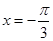 时取得最小值-4.
时取得最小值-4.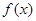 的解析式;
的解析式;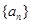 前n项和为
前n项和为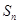 ,且
,且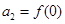 ,
, ,求数列
,求数列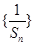 的前n项和
的前n项和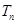 .
.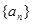 中,
中,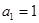 ,且
,且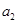 是
是 和
和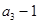 的等差中项.
的等差中项.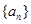 的通项公式;
的通项公式;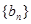 满足
满足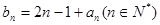 ,求
,求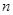 项和
项和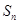 .
.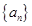 的前
的前 项和为
项和为 ,且满足
,且满足 ,其中
,其中 、
、 、
、 是常数.
是常数. ,
, ,
, ,求数列
,求数列 ,
, ,
, ,且
,且 ,求数列
,求数列 的等比数列.
的等比数列. 满足:
满足: ,该数列的前三项分别加上l,l,3后顺次成为等比数列
,该数列的前三项分别加上l,l,3后顺次成为等比数列 的前三项.
的前三项. ,若
,若 恒成立,求c的最小值.
恒成立,求c的最小值.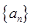 满足:
满足: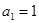 ,
,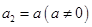 ,
,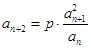 (其中
(其中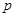 为非零常数,
为非零常数,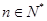 ).
).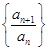 是不是等比数列?
是不是等比数列?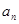 ;
;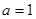 时,令
时,令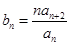 ,
,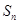 为数列
为数列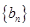 的前
的前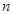 项和,求
项和,求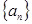 的前
的前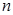 项和
项和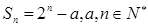 .设公差不为零的等差数列
.设公差不为零的等差数列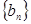 满足:
满足: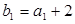 ,且
,且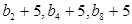 成等比.
成等比.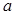 及
及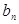 ;
;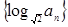 的前
的前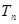 .求使
.求使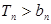 的最小正整数
的最小正整数