题目内容
18. 如图,在平面直角坐标系中,分别在x轴与直线$y=\frac{{\sqrt{3}}}{3}({x+1})$上从左向右依次取点Ak、Bk,k=1,2,…,其中A1是坐标原点,使△AkBkAk+1都是等边三角形,则△A10B10A11的边长是512.
如图,在平面直角坐标系中,分别在x轴与直线$y=\frac{{\sqrt{3}}}{3}({x+1})$上从左向右依次取点Ak、Bk,k=1,2,…,其中A1是坐标原点,使△AkBkAk+1都是等边三角形,则△A10B10A11的边长是512.
分析 设直线与x轴交点坐标为P,由直线$y=\frac{{\sqrt{3}}}{3}({x+1})$的倾斜角为300,又△A1B1A2是等边三角形$\sqrt{3}$,求出△A2B2A3、…找出规律,就可以求出△A10B10A11的边长.
解答 解:∵直线$y=\frac{{\sqrt{3}}}{3}({x+1})$的倾斜角为300,且直线与x轴交点坐标为P(-1,0),
又∵△A1B1A2是等边三角形,∴∠B1A1A2=600,B1A1=1,PA2=2,
∴△A2B2A3的边长为PA2=2,同理 B2A2=PA3=4,…以此类推
B10A10=PA10=512,∴△A10B10A11的边长是512,
故答案为:512.
点评 本题考查了直线的倾斜角,等边三角形的性质,及归纳推理的能力,属于基础题.

练习册系列答案
相关题目
9.在考试测评中,常用难度曲线图来检测题目的质量,一般来说,全卷得分高的学生,在某道题目上的答对率也应较高,如果是某次数学测试压轴题的第1、2问得分难度曲线图,第1、2问满分均为6分,图中横坐标为分数段,纵坐标为该分数段的全体考生在第1、2问的平均难度,则下列说法正确的是( )
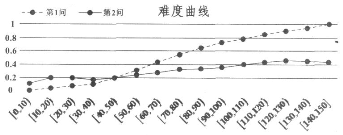

| A. | 此题没有考生得12分 | |
| B. | 此题第1问比第2问更能区分学生数学成绩的好与坏 | |
| C. | 分数在[40,50)的考生此大题的平均得分大约为4.8分 | |
| D. | 全体考生第1问的得分标准差小于第2问的得分标准差 |
6.关于函数f(x)=x3-3x2+6x的单调性是( )
| A. | 增函数 | B. | 先增后减 | C. | 先减后增 | D. | 减函数 |
10.已知△ABC的面积为$\sqrt{3}$,且∠C=30°,BC=2$\sqrt{3}$,则AB等于( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
7.已知集合A={-1,1},B={1,-1,3},那么A∩B=等于( )
| A. | {-1} | B. | {1} | C. | {-1,1} | D. | {1,-1,3} |