题目内容
9.已知函数f(x)=$\frac{1}{2}$ax2-(a+2)x+2lnx(a∈R).(1)若a=0,证明:f(x)<0;
(2)讨论函数f(x)零点的个数.
分析 (1)将a=0代入函数的表达式,求出f′(x),解关于导函数的不等式,求出函数的单调区间,得到最大值是f(1)<0即可;
(2)先求出函数的导数,通过讨论a的范围,从而求出函数的单调区间,得到函数的极值,进而求出函数的零点的个数.
解答 解:(1)a=0时:f(x)=-2x+2lnx,(x>0),
f′(x)=-2+$\frac{2}{x}$=$\frac{2(1-x)}{x}$,
令f′(x)>0,解得:0<x<1,令f′(x)<0,解得:x>1,
∴f(x)在(0,1)递增,在(1,+∞)递减,
∴f(x)最大值=f(1)=-2+2ln1=-2<0,
∴a=0时,f(x)<0;
(2)f′(x)=$\frac{2}{x}$+ax-(a+2)=$\frac{(ax-2)(x-1)}{x}$,(x>0),
①a≤0时,ax-2<0
令f′(x)>0,解得:0<x<1,令f′(x)<0,解得:x>1,
∴f(x)在(0,1)递增,在(1,+∞)递减;
若a<-4,f(x)max=f(1)=-$\frac{1}{2}$-2>0,函数f(x)有2个零点,
若a=-4,f(x)max=f(1)=-$\frac{1}{2}$-2,=0,函数f(x)有1个零点,
若-4<a≤0,f(x)max=f(1)=-$\frac{1}{2}$-2<0,函数f(x)没有零点,
②0<a<2时,$\frac{2}{a}$>1,
令f′(x)>0,解得:x>$\frac{2}{a}$,或0<x<1,
令f′(x)<0,解得:1<x<$\frac{2}{a}$,
∴f(x)在(0,1),($\frac{2}{a}$,+∞)递增,在(1,$\frac{2}{a}$)递减;
∴f(x)极大值=f(1)=-$\frac{1}{2}$a-2<0,
∴f(x)有1个零点;
③a≥2时,$\frac{2}{a}$<1,
令f′(x)>0,解得:x>1,或0<x<$\frac{2}{a}$,
令f′(x)<0,解得:$\frac{2}{a}$<x<1,
∴f(x)在(0,$\frac{2}{a}$),(1,+∞)递增,在($\frac{2}{a}$,1)递减;
∴f(x)极大值=f($\frac{2}{a}$)=-$\frac{2(a+1)}{a}$+2ln$\frac{2}{a}$<0,
∴f(x)有1个零点.
点评 本题考查了函数的单调性、最值、零点问题,考查导数的应用,是一道中档题.

 如图所示是三棱锥D-ABC的三视图,若在三棱锥的直观图中,点O为线段BC的中点,则异面直线DC与AB所成角的余弦值等于( )
如图所示是三棱锥D-ABC的三视图,若在三棱锥的直观图中,点O为线段BC的中点,则异面直线DC与AB所成角的余弦值等于( )| A. | $\frac{{\sqrt{6}}}{6}$ | B. | $\frac{{\sqrt{6}}}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
 如图,在△ABC中,AB=2,AC=4,线段CB的垂直平分线交线段AC于D,AD-DB=1,则△BCD的面积为( )
如图,在△ABC中,AB=2,AC=4,线段CB的垂直平分线交线段AC于D,AD-DB=1,则△BCD的面积为( )| A. | $\frac{7}{10}$ | B. | $\frac{9}{10}$ | C. | 2 | D. | 8 |
| A. | [1,3] | B. | [$\sqrt{5}$-1,$\sqrt{5}$十1] | C. | [3-2$\sqrt{2}$,3+2$\sqrt{2}$] | D. | [4-2$\sqrt{3}$,4+2$\sqrt{3}$]. |
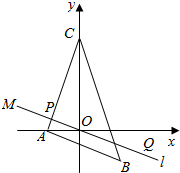 如图所示,已知A(-2,0),B(2,-2),C(0,5),过点M(-4,2)且平行于AB的直线l将△ABC分成两部分,求此两部分面积的比值.
如图所示,已知A(-2,0),B(2,-2),C(0,5),过点M(-4,2)且平行于AB的直线l将△ABC分成两部分,求此两部分面积的比值.