题目内容
4.将8个珠子(4个黑珠子和4个白珠子)排成一行,从左边第一小珠开始向右数珠子,无论数几个珠子,黑珠子的个数总不少于白珠子个数的概率为$\frac{1}{5}$.分析 将8个珠子(4个黑珠子和4个白珠子)排成一行,先求出基本事件总数,再由求出,由此能求出无论数几个珠子,黑珠子的个数总不少于白珠子个数包含的基本事件个数,由此能求出无论数几个珠子,黑珠子的个数总不少于白珠子个数的概率.
解答 解:将8个珠子(4个黑珠子和4个白珠子)排成一行,
基本事件总数为n=${A}_{8}^{8}$,
∵从左边第一小珠开始向右数珠子,无论数几个珠子,黑珠子的个数总不少于白珠子个数,
∴8个球的排列顺序有:(1)黑白黑白黑白黑白;(2)黑黑白白黑黑白白;(3)黑黑黑白白白黑白;
(4)黑黑黑黑白白白白;(5)黑白黑黑白白黑白;(6)黑黑白白黑白黑白;(7)黑白黑白黑黑白白;
(8)黑白黑黑黑白白白;(9)黑黑白黑白黑白白;(10)黑黑黑白白黑白白;(11)黑黑白黑黑白白白;
(12)黑黑黑白黑白白白;(13)黑白黑黑白黑白白;(14)黑黑白黑白白黑白.
∴无论数几个珠子,黑珠子的个数总不少于白珠子个数的概率:
p$\frac{{A}_{4}^{4}{A}_{4}^{4}×14}{{A}_{8}^{8}}$=$\frac{1}{5}$.
故答案为:$\frac{1}{5}$.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
12.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2},x≤0}\\{{-x}^{2},x>0}\end{array}\right.$,不等式f(ax2)+f(1-ax)<0对任意的x∈R都成立,则实数a的取值范围( )
| A. | (0,4) | B. | (-4,0) | C. | [0,4) | D. | [0,4] |
19.已知集合M={x|$\frac{1}{2-x}$>0},N={1,2,3,4},则∁RM∩N=( )
| A. | {1,2,3,4} | B. | {2,3,4} | C. | {1} | D. | ∅ |
13.复数$\frac{3-i}{i}$=( )
| A. | 1+3i | B. | -1-3i | C. | -1+3i | D. | 1-3i |
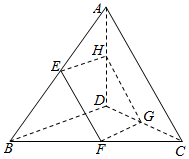 如图,在空间四边形ABCD中,E,F,G,H分别是AB,BC,DA的中点,且AC=BC.求证:四边形EFGH是菱形.
如图,在空间四边形ABCD中,E,F,G,H分别是AB,BC,DA的中点,且AC=BC.求证:四边形EFGH是菱形.