题目内容
1．已知函数f（x）=$\left\{\begin{array}{l}{{2}^{x}+1，x≤1}\\{lo{g}_{3}（x+1），x＞1}\end{array}\right.$，则f[f（2）]=3．分析 先求出f（2）的值，从而求出f（f（2））的值即可．
解答 解f（2）=${log}_{3}^{2+1}$=1，
∴f（f（2））=f（1）=21+1=3，
故答案为：3．
点评 本题考查了函数求值问题，考查对数、指数的运算，是一道基础题．
练习册系列答案
阅读快车系列答案
相关题目
11．口袋中有编号分别为1、2、3的三个大小和形状相同的小球，从中任取2个，则取出的球的最大编号X的均值为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{2}{3}$ | C． | 2 | D． | $\frac{8}{3}$ |
12．下列程序输出的结果是（ ）
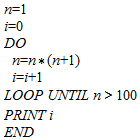
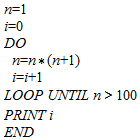
| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
16．设i是虚数单位，则复数$\frac{3+4i}{1-i}$的共轭复数为（ ）
| A． | -$\frac{1}{2}$+$\frac{7}{2}$i | B． | -$\frac{1}{2}$-$\frac{7}{2}$i | C． | $\frac{1}{2}$-$\frac{7}{2}$i | D． | $\frac{1}{2}$+$\frac{7}{2}$i |
6．若（x+$\frac{a}{{x}^{2}}$）9的二项展开式中含x6项的系数是36，则实数a=（ ）
| A． | 1 | B． | -1 | C． | $\frac{\sqrt{2}}{2}$ | D． | 4 |