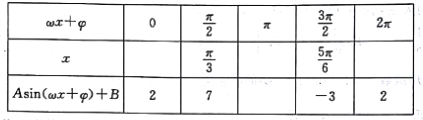
题目内容
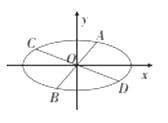
【题目】椭圆 ![]() 的经过中心的弦称为椭圆的一条直径,平行于该直径的所有弦的中点的轨迹为一条线段,称为该直径的共轭直径,已知椭圆的方程为
的经过中心的弦称为椭圆的一条直径,平行于该直径的所有弦的中点的轨迹为一条线段,称为该直径的共轭直径,已知椭圆的方程为 ![]() .
.
(1)若一条直径的斜率为 ![]() ,求该直径的共轭直径所在的直线方程;
,求该直径的共轭直径所在的直线方程;
(2)若椭圆的两条共轭直径为 ![]() 和
和 ![]() ,它们的斜率分别为
,它们的斜率分别为 ![]() ,证明:四边形
,证明:四边形 ![]() 的面积为定值.
的面积为定值.
【答案】
(1)解:设斜率为 ![]() 的与直径平行的弦的端点坐标分别为
的与直径平行的弦的端点坐标分别为 ![]() ,
, ![]() ,
,
该弦中点为 ![]() ,则有
,则有 ![]() ,
, ![]() ,
,
相减得: ![]() ,
,
由于 ![]() ,
, ![]() ,且
,且 ![]() ,所以得:
,所以得: ![]() ,
,
故该直径的共轭直径所在的直线方程为 ![]()
(2)解:椭圆的两条共轭直径为 ![]() 和
和 ![]() ,它们的斜率分别为
,它们的斜率分别为 ![]() ,
,
四边形 ![]() 显然为平行四边形,设与
显然为平行四边形,设与 ![]() 平行的弦的端点坐标分别为
平行的弦的端点坐标分别为 ![]()
则 ![]() ,
, ![]() ,而
,而 ![]() ,
, ![]() ,
,![]() ,故
,故 ![]() ,
,
由 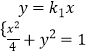 得
得 ![]() 的坐标分别为
的坐标分别为 ![]() ,
, ![]()
故 ![]() ,同理
,同理 ![]() 的坐标分别为
的坐标分别为 ![]() ,
, ![]()
设点 ![]() 到直线
到直线 ![]() 的距离为
的距离为 ![]() ,四边形
,四边形 ![]() 的面积为
的面积为 ![]() ,
,
所以, 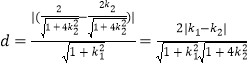 ,
,
则 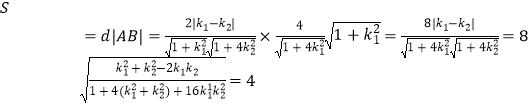 ,为定值
,为定值
【解析】(1)考查中点弦问题 ,利用点差法求出直线方程 。
(2)设出直线方程,求出弦长![]() ,再求出点 C 到直线 A B 的距离为 d,求四边形 A C B D 的面积为 S 。
,再求出点 C 到直线 A B 的距离为 d,求四边形 A C B D 的面积为 S 。

练习册系列答案
相关题目