题目内容
已知函数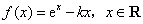 .
.
(1)若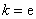 ,试确定函数
,试确定函数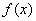 的单调区间;
的单调区间;
(2)若 ,且对于任意
,且对于任意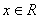 ,
,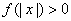 恒成立,试确定实数
恒成立,试确定实数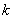 的取值范围;
的取值范围;
(3)设函数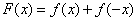 ,求证:
,求证: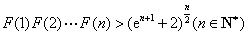 .
.
解:(1)由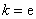 得
得 ,所以
,所以 .
.
由 得
得 ,故
,故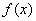 的单调递增区间是
的单调递增区间是 ,
,
由 得
得 ,故
,故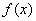 的单调递减区间是
的单调递减区间是
(2)由 可知:
可知: 是偶函数.
是偶函数.
于是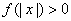 对任意
对任意 成立等价于
成立等价于 对任意
对任意 成立
成立
由 得
得 .
.
①当 时,
时, .此时
.此时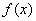 在
在 上单调递增.故
上单调递增.故 ,符合题意.
,符合题意.
②当 时,
时, .
.
当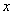 变化时
变化时 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
| 单调递减 | 极小值 | 单调递增 |
由此可得,在 上,
上, .
.
依题意得: ,又
,又 .
.
综合①,②得,实数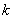 的取值范围是:
的取值范围是: .
.
(3) ,
,


 ,
,

由此得:
故 .
.

练习册系列答案
相关题目



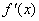



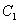 :
: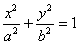 (
(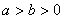 )和圆
)和圆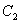 :
: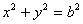 ,已知圆
,已知圆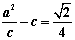 ,椭圆
,椭圆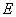 ,过坐标原点
,过坐标原点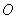 且与坐标轴不重合的任意直线
且与坐标轴不重合的任意直线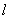 与圆
与圆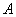 、
、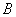 .
.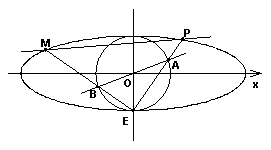 (Ⅰ )求椭圆
(Ⅰ )求椭圆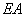 、
、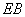 分别与椭圆
分别与椭圆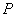 、
、 .
. 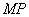 经过一定点;
经过一定点; 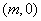 为圆心,
为圆心,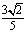 为半径的圆
为半径的圆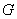 ,使得直线
,使得直线 和直线
和直线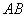 都与圆
都与圆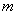 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. , 则z等于
, 则z等于 ,且当
,且当 试判断函数的奇偶性与单调性,证明你的结论.
试判断函数的奇偶性与单调性,证明你的结论. .设发病的牛的头数为
.设发病的牛的头数为 ,则
,则 等于
等于 B.
B. C.
C. D.
D.
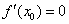 ,则函数
,则函数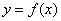 在
在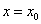 取得极值;
取得极值;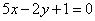 与函数
与函数 的图像不相切;
的图像不相切;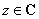 (
( 为复数集),且
为复数集),且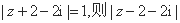 的最小值是
的最小值是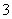 ;
; .
. 各角的对应边分别为
各角的对应边分别为 ,满足
,满足 ,则角
,则角 的范围是( )
的范围是( ) B.
B. C.
C. D.
D.
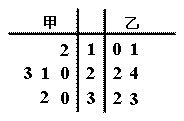 2015赛季CBA(中国男子职业篮球联赛)总决赛于3月22号结束,北京首钢队4∶2战胜辽宁药都队卫冕成功。如图是参加此次总决赛的甲、乙两名运动员在6场比赛中的得分茎叶图,两人得分的平均数分别为
2015赛季CBA(中国男子职业篮球联赛)总决赛于3月22号结束,北京首钢队4∶2战胜辽宁药都队卫冕成功。如图是参加此次总决赛的甲、乙两名运动员在6场比赛中的得分茎叶图,两人得分的平均数分别为 、
、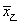 ,得分的标准差分别为
,得分的标准差分别为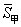 、
、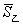 ,则下面正确的结论是( )
,则下面正确的结论是( )