题目内容
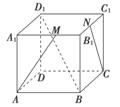
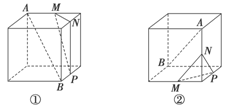
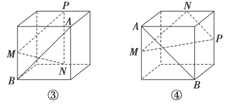
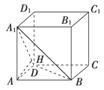
如图所示，等腰直角三角形ABC中，∠A＝90°，BC＝
，DA⊥AC，DA⊥AB，若DA＝1，且E为DA的中点．求异面直线BE与CD所成角的余弦值．
解：取AC的中点F，连接EF，BF，
在△ACD中，E、F分别是AD、AC的中点，
∴EF∥CD.
∴∠BEF即为异面直线BE与CD所成的角或其补角．
在Rt△EAB中，AB＝AC＝1，
AE＝
AD＝，
∴BE＝
.
在Rt△EAF中，AF＝AC＝，AE＝，
∴EF＝
.
在Rt△BAF中，AB＝1，AF＝，∴BF＝.
在等腰三角形EBF中，cos∠FEB＝
＝
，
∴异面直线BE与CD所成角的余弦值为.
练习册系列答案
全能练考卷系列答案
一课一练课时达标系列答案
相关题目
(a≥0)，则P、Q的大小关系是( )
B.
条数为( )
某初级中学共有学生2000名，各年级男、女生人数如下表：
|
| 初一年级 | 初二年级 | 初三年级 |
| 女生 | 373 | x | y |
| 男生 | 377 | 370 | z |
已知在全校学生中随机抽取1名，抽到初二年级女生的概率是0.19.
(1)求x的值；
(2)现用分层抽样的方法在全校抽取48名学生，问应在初三年级抽取多少名？
(3)已知y≥245，z≥245，求初三年级中女生比男生多的概率．