题目内容
17．已知直线l：x-2y+4=0与点P（2，1），分别写出满足下列条件的直线方程：（1）过点P且与直线l平行；
（2）过点P且与直线l垂直．
分析 （1）根据已知直线l的解析式可以求得直线l的斜率为$\frac{1}{2}$，然后设所求直线为点斜式，利用待定系数法解答即可；
（2）根据已知直线l的解析式可以求得直线l的斜率为-2，然后设所求直线为点斜式，利用待定系数法解答即可．
解答 解：（1）因为两直线互相平行，且${k_l}=\frac{1}{2}$，所以所求直线的斜率为$\frac{1}{2}$，
故所求直线的方程$y-1=\frac{1}{2}（x-2）$，即x-2y=0；
（2）因为两直线互相垂直，所以所求直线的斜率为-2，
故所求直线的方程y-1=-2（x-2），即2x+y-5=0．
点评 本题主要考查利用两直线平行、垂直的性质，用待定系数法求直线方程，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
7．化简$\frac{sin（2π-α）cos（π+α）cos（\frac{π}{2}+α）cos（\frac{11π}{2}-α）}{cos（π-α）sin（3π-α）sin（-π-α）sin（\frac{9π}{2}+α）}$的结果是（ ）
| A． | 1 | B． | sinα | C． | -tanα | D． | tanα |
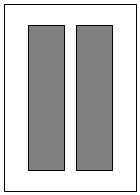如图，要设计一张矩形广告牌，该广告牌含有大小相等的左右两个矩形栏目（即图中阴影部分），这两栏的面积之和为18000cm2，四周空白的宽度为10cm，两栏之间的中缝空白的宽度为5cm，设广告牌的高为xcm，宽为ycm
6．定义在R上的函数f（x）既是奇函数又是周期函数，若f（x）的最小正周期是π，且当$x∈[0，\frac{π}{2}）$时，f（x）=sinx，则$f（\frac{8}{3}π）$的值为（ ）
| A． | $\frac{1}{2}$ | B． | $-\frac{{\sqrt{3}}}{2}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | $-\frac{1}{2}$ |