题目内容
已知F1、F2双曲线
-
=1(a>0,b>0)的两焦点,O是坐标原点,直线AB过F1,且垂直于x轴,并与双曲线交于A、B两点,若AO⊥BF2,则双曲线的离心率e=( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
分析:先由题意得:F1(-c,0),F2(c,0),A(-c,
),B(-c,-
),从而得到直线AO,直线BF2的斜率,结合AO⊥BF2,有:k1k2=-1,从而建立a与c的关系,最后即可求得双曲线的离心率.
| b2 |
| a |
| b2 |
| a |
解答:解:由题意得:F1(-c,0),F2(c,0),
A(-c,
),B(-c,-
),
∴直线AO的斜率k1=
=-
,直线BF2的斜率k2=
=
,
∵AO⊥BF2,
∴k1k2=-1,即-
×
=-1
∴b4=2a2c2,又b2=c2-a2,
∴(c2-a2)2=2a2c2,
解之得:
=
故选C.
A(-c,
| b2 |
| a |
| b2 |
| a |
∴直线AO的斜率k1=
| ||
| -c |
| b2 |
| ac |
-
| ||
| -2c |
| b2 |
| 2ac |
∵AO⊥BF2,
∴k1k2=-1,即-
| b2 |
| ac |
| b2 |
| 2ac |
∴b4=2a2c2,又b2=c2-a2,
∴(c2-a2)2=2a2c2,
解之得:
| c |
| a |
| ||||
| 2 |
故选C.
点评:本题考查了直线与圆锥曲线的综合问题以及双曲线的简单性质,由双曲线几何性质和AO⊥BF2,,能够得出b4=2a2c2是解题的关键,属于中档题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 的两焦点,O是坐标原点,直线AB过F1,且垂直于x轴,并与双曲线交于A、B两点,若AO⊥BF2,则双曲线的离心率e=
的两焦点,O是坐标原点,直线AB过F1,且垂直于x轴,并与双曲线交于A、B两点,若AO⊥BF2,则双曲线的离心率e=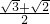
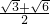
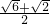

 的两焦点,O是坐标原点,直线AB过F1,且垂直于x轴,并与双曲线交于A、B两点,若AO⊥BF2,则双曲线的离心率e=( )
的两焦点,O是坐标原点,直线AB过F1,且垂直于x轴,并与双曲线交于A、B两点,若AO⊥BF2,则双曲线的离心率e=( )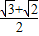

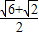
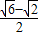
 的左、右焦点,直线
的左、右焦点,直线 与C在一象限的交点为P,点Q在线段PF2的延长线上,|PF1|=|PQ|,则△F1F2Q的面积是 .
与C在一象限的交点为P,点Q在线段PF2的延长线上,|PF1|=|PQ|,则△F1F2Q的面积是 .