题目内容
已知F1、F2双曲线C:
-
=1的左、右焦点,直线l:y=
(x-5)与C在一象限的交点为P,点Q在线段PF2的延长线上,|PF1|=|PQ|,则△F1F2Q的面积是
| x2 |
| 16 |
| y2 |
| 9 |
| ||
| 3 |
20
20
.分析:利用双曲线的定义转化可求得F2Q,再利用点到直线间的距离公式求得点F1到直线l的距离(△F1F2Q的底边F2Q上的高)即可求得△F1F2Q的面积.
解答:解:∵双曲线C的方程为:
-
=1,左、右焦点分别为F1(-5,0)、F2(5,0),点P在右支上,
∴|PF1|-|PF2|=2a=8,
又|F2Q|=|PQ|-|PF2|,|PF1|=|PQ|,
∴|F2Q|=|PF1|-|PF2|=8,
设点F1到直线l:y=
(x-5)即
x-3y-5
=0的距离为d,
则:d=
=
=5,
∴△F1F2Q的面积S=
|F2Q|d=
×8×5=20.
故答案为:20.
| x2 |
| 16 |
| y2 |
| 9 |
∴|PF1|-|PF2|=2a=8,
又|F2Q|=|PQ|-|PF2|,|PF1|=|PQ|,
∴|F2Q|=|PF1|-|PF2|=8,
设点F1到直线l:y=
| ||
| 3 |
| 3 |
| 3 |
则:d=
|
| ||||
|
10
| ||
2
|
∴△F1F2Q的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:20.
点评:本题考查双曲线的定义及点到直线间的距离公式、三角形的面积公式,考查转化思想与运算能力,属于中档题.

练习册系列答案
相关题目
已知F1、F2双曲线
-
=1(a>0,b>0)的两焦点,O是坐标原点,直线AB过F1,且垂直于x轴,并与双曲线交于A、B两点,若AO⊥BF2,则双曲线的离心率e=( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 的两焦点,O是坐标原点,直线AB过F1,且垂直于x轴,并与双曲线交于A、B两点,若AO⊥BF2,则双曲线的离心率e=
的两焦点,O是坐标原点,直线AB过F1,且垂直于x轴,并与双曲线交于A、B两点,若AO⊥BF2,则双曲线的离心率e=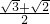
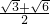
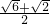

 的两焦点,O是坐标原点,直线AB过F1,且垂直于x轴,并与双曲线交于A、B两点,若AO⊥BF2,则双曲线的离心率e=( )
的两焦点,O是坐标原点,直线AB过F1,且垂直于x轴,并与双曲线交于A、B两点,若AO⊥BF2,则双曲线的离心率e=( )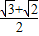

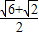
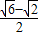
 的左、右焦点,直线
的左、右焦点,直线 与C在一象限的交点为P,点Q在线段PF2的延长线上,|PF1|=|PQ|,则△F1F2Q的面积是 .
与C在一象限的交点为P,点Q在线段PF2的延长线上,|PF1|=|PQ|,则△F1F2Q的面积是 .