题目内容
如图，在四棱锥
中，已知
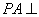平面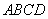
，
且四边形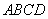为直角梯形，
,
.
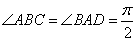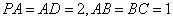（1）求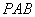平面
与平面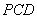
所成二面角的余弦值；
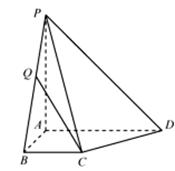
（2）点Q是线段BP上的动点，当直线CQ与DP所成角最小时，求线
段BQ的长
练习册系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
相关题目
黄冈360度定制密卷系列答案阳光考场单元测试卷系列答案名校联盟冲刺卷系列答案名校提分一卷通系列答案题目内容
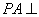如图，在四棱锥中，已知平面，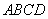
且四边形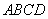为直角梯形，,.
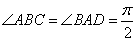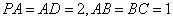（1）求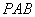平面与平面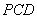所成二面角的余弦值；
（2）点Q是线段BP上的动点，当直线CQ与DP所成角最小时，求线段BQ的长
黄冈360度定制密卷系列答案阳光考场单元测试卷系列答案名校联盟冲刺卷系列答案名校提分一卷通系列答案
的二项展开式中x3的系数为_________. 
除以9的余数
是 
这五个数中,每次取出两个不同的数分别为
,共可得到
的不同值的个数是 
机变量Z的分布列为
若
则
的分布列如右表．若
，
，则a、b、c的值依次
为 .
中，
为不等式组
，所表示的区域上的一动点，则直线
的斜率的最小值为( )
B. 1 C. 
D.
：
（
）的焦距为
，且过点（
，
），右焦点为
．设
，
是
的中点
的横坐标为
，
线段
，
两点．
（Ⅰ）求椭圆
的取值范围．