题目内容
在平面上,
⊥
,|
|=|
|=1,
=
+
,若|
|<
,则|
|的取值范围是 .
| AB1 |
| AB2 |
| OB1 |
| OB2 |
| AP |
| AB1 |
| AB2 |
| OP |
| 1 |
| 2 |
| OA |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:根据
⊥
,|
|=|
|=1,
=
+
,可知:四边形AB1PB2是一个矩形.以AB1,AB2所在直线为坐标轴建立直角坐标系.设|AB1|=a,|AB2|=b.点O的坐标为(x,y),点P(a,b).根据向量的坐标运算、模的计算公式、不等式的性质即可得出.
| AB1 |
| AB2 |
| OB1 |
| OB2 |
| AP |
| AB1 |
| AB2 |
解答:
解:根据
⊥
,
=
+
,可知:四边形AB1PB2是一个矩形.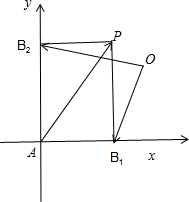
以AB1,AB2所在直线为坐标轴建立直角坐标系.设|AB1|=a,|AB2|=b.
点O的坐标为(x,y),点P(a,b).
∵|
|=|
|=1,
∴
,
变形为
.
∵|
|<
,∴(x-a)2+(y-b)2<
,
∴1-x2+1-y2
,
∴x2+y2>
.①
∵(x-a)2+y2=1,∴y2≤1.
同理,x2≤1.
∴x2+y2≤2.②
由①②可知:
<x2+y2≤2.
∵|
|=
,
∴
<|
≤
.
故答案为(
,
].
| AB1 |
| AB2 |
| AP |
| AB1 |
| AB2 |

以AB1,AB2所在直线为坐标轴建立直角坐标系.设|AB1|=a,|AB2|=b.
点O的坐标为(x,y),点P(a,b).
∵|
| OB1 |
| OB2 |
∴
|
变形为
|
∵|
| OP |
| 1 |
| 2 |
| 1 |
| 4 |
∴1-x2+1-y2
| 1 |
| 4 |
∴x2+y2>
| 7 |
| 4 |
∵(x-a)2+y2=1,∴y2≤1.
同理,x2≤1.
∴x2+y2≤2.②
由①②可知:
| 7 |
| 4 |
∵|
| OA |
| x2+y2 |
∴
| ||
| 2 |
| OA| |
| 2 |
故答案为(
| ||
| 2 |
| 2 |
点评:本题考查了向量的平行四边形法则、矩形的定义、向量的坐标运算、模的计算公式、不等式的性质,考查了数形结合的思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
已知△ABC中,|
|=2,|
|=3,且△ABC的面积为
,则∠BAC=( )
| AB |
| AC |
| 3 |
| 2 |
| A、150° |
| B、120° |
| C、60°或120° |
| D、30°或150° |
已知函数f(x)=x|x-a|+2x,若存在a∈[0,4],使得关于x的方程f(x)=tf(a)有三个不相等的实数根,则实数t的取值范围是( )
A、(1,
| ||||
B、(1,
| ||||
C、(
| ||||
D、(1,
|
关于函数f(x)=2(sinx-cosx)cosx的四个结论:
P1:最大值为
;
P2:最小正周期为π;
P3:单调递增区间为[kπ-
,kπ+
π],k∈Z;
P4:函数y=f(x)的一条对称轴是x=
其中正确的有( )
P1:最大值为
| 2 |
P2:最小正周期为π;
P3:单调递增区间为[kπ-
| π |
| 8 |
| 3 |
| 8 |
P4:函数y=f(x)的一条对称轴是x=
| 7π |
| 8 |
其中正确的有( )
| A、1 个 | B、2个 |
| C、3个 | D、4个 |
若loga
<1,则a的取值范围是( )
| 1 |
| 3 |
A、(0,
| ||||
B、(
| ||||
C、(
| ||||
D、(0,
|
执行如图所示框图,则输出S的值为( )


A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|