Question

【题目】如图，在四棱锥中，平面，底面为菱形，且，，、分别为、中点．

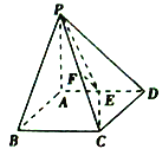
（1）求点到平面的距离；

（2）求证：平面平面．

Answer 1

【答案】（1）;（2）见解析.

【解析】【试题分析】（1）借助题设与已知条件运用等价转化的数学思想将点到面的距离转化为另一个点到平面的距离；（2）依据题设条件，先运用线面垂直的判定定理证明线面垂直，进而运用面面垂直的判定定理证明面面垂直。

（1）解：如图，

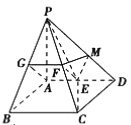
取的中点，连接、，

因为底面为菱形，且，，

所以底面为正方形．

∵、分别为、中点，

∴，，，，

∴且，∴四边形是平行四边形，∴，

∵平面，平面，∴平面，

∴点与点到平面的距离相等，即距离为．

（2）证明：由（1）知，，

∵平面，∴，

∵，，∴平面，

∴，又∵，

∴平面，∴平面，

∵平面，∴平面平面．