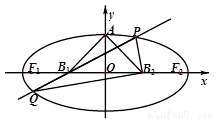
题目内容
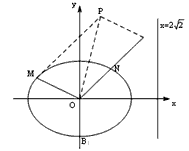
如图,椭圆的中心为原点O,离心率e=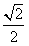 ,一条准线的方程是x=
,一条准线的方程是x=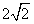 ,
,
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设动点P满足: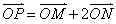 ,其中M,N是椭圆上的点,直线OM与ON的斜率之积为
,其中M,N是椭圆上的点,直线OM与ON的斜率之积为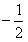 。问:是否存在定点F,使得|PF|与点P到直线l:x=
。问:是否存在定点F,使得|PF|与点P到直线l:x=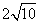 的距离之比为定值?若存在,求F的坐标;若不存在,说明理由。
的距离之比为定值?若存在,求F的坐标;若不存在,说明理由。
解:(Ⅰ)∵ ,
, ,解得a=2,c=
,解得a=2,c= ,
,
∴b2=a2-c2=2,
∴椭圆的标准方程为 ;
;
(Ⅱ)设P(x,y), ,
,
则由 ,得
,得 ,
,
∴x= ,y=
,y= ,
,
∵M,N在椭圆 上,
上,
∴ ,
,
∴
 ,
,
设 分别表示直线OM,ON的斜率,
分别表示直线OM,ON的斜率,
由题设条件知, ,
,
∴ ,
,
∴ =20,
=20,
∴点P在椭圆 上,
上,
该椭圆的右焦点为F( ,0),离心率e=
,0),离心率e= ,右准线为l:x=2
,右准线为l:x=2 ,
,
∴根据椭圆的第二定义,存在定点F( ,0),使得|PF|与点P到直线l的距离之比为定值。
,0),使得|PF|与点P到直线l的距离之比为定值。
 ,
, ,解得a=2,c=
,解得a=2,c= ,
,∴b2=a2-c2=2,
∴椭圆的标准方程为
 ;
;(Ⅱ)设P(x,y),
 ,
,则由
 ,得
,得 ,
,∴x=
 ,y=
,y= ,
,∵M,N在椭圆
 上,
上,∴
 ,
,∴

 ,
,设
 分别表示直线OM,ON的斜率,
分别表示直线OM,ON的斜率,由题设条件知,
 ,
,∴
 ,
,∴
 =20,
=20,∴点P在椭圆
 上,
上,该椭圆的右焦点为F(
 ,0),离心率e=
,0),离心率e= ,右准线为l:x=2
,右准线为l:x=2 ,
,∴根据椭圆的第二定义,存在定点F(
 ,0),使得|PF|与点P到直线l的距离之比为定值。
,0),使得|PF|与点P到直线l的距离之比为定值。 
练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
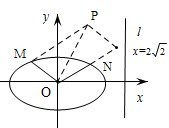 如图,椭圆的中心为原点O,离心率e=
如图,椭圆的中心为原点O,离心率e=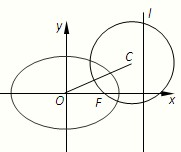 如图,椭圆的中心为原点O,已知右准线l的方程为x=4,右焦点F到它的距离为2.
如图,椭圆的中心为原点O,已知右准线l的方程为x=4,右焦点F到它的距离为2.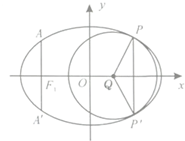 (2013•重庆)如图,椭圆的中心为原点O,长轴在x轴上,离心率
(2013•重庆)如图,椭圆的中心为原点O,长轴在x轴上,离心率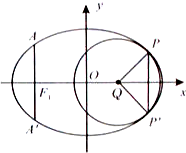 (2013•重庆)如图,椭圆的中心为原点O,长轴在x轴上,离心率
(2013•重庆)如图,椭圆的中心为原点O,长轴在x轴上,离心率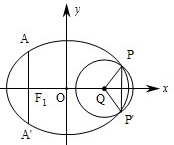
 ,线段
,线段 的中点分别为
的中点分别为 ,且△
,且△ 是面积为4的直角三角形.
是面积为4的直角三角形. 做直线
做直线 交椭圆于P,Q两点,使
交椭圆于P,Q两点,使 ,求直线
,求直线