题目内容
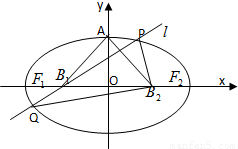
如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左右焦点分别为 ,线段
,线段 的中点分别为
的中点分别为 ,且△
,且△ 是面积为4的直角三角形.
是面积为4的直角三角形.
(Ⅰ)求该椭圆的离心率和标准方程;
(Ⅱ)过 做直线
做直线 交椭圆于P,Q两点,使
交椭圆于P,Q两点,使 ,求直线
,求直线 的方程.
的方程.
【答案】
(I)所求椭圆的标准方程为: 
(2)满足条件的直线有两条,其方程分别为: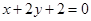 和
和
【解析】(I) 设所求椭圆的标准方程为 ,因
,因 是直角三角形,又
是直角三角形,又 ,故
,故 为直角,因此
为直角,因此 ,得
,得 .又因为
.又因为 ,消去b可得a,c的一个等式关系,从而可求出离心率,再利用
,消去b可得a,c的一个等式关系,从而可求出离心率,再利用 ,求出b,进而可得到a的值,椭圆方程确定.
,求出b,进而可得到a的值,椭圆方程确定.
(II) 由(1)知 ,由题意知直线
,由题意知直线 的倾斜角不为0,故可设直线
的倾斜角不为0,故可设直线 的方程为:
的方程为: ,代入椭圆方程得
,代入椭圆方程得 ,
,
因为 ,所以
,所以

 =0
=0
然后借助韦达定理代入上式可得关于m的方程求出m值,得到直线l的方程

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
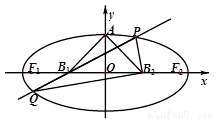
 (2012•重庆)如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左右焦点分别为F1,F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为4的直角三角形.
(2012•重庆)如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左右焦点分别为F1,F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为4的直角三角形. (2012•重庆)如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1,F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为4的直角三角形.
(2012•重庆)如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1,F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为4的直角三角形.