题目内容
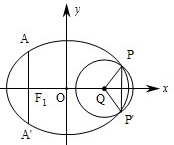
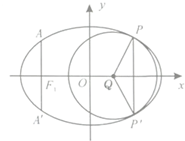 (2013•重庆)如图,椭圆的中心为原点O,长轴在x轴上,离心率e=
(2013•重庆)如图,椭圆的中心为原点O,长轴在x轴上,离心率e=
| ||
| 2 |
(Ⅰ)求该椭圆的标准方程;
(Ⅱ)取平行于y轴的直线与椭圆相交于不同的两点P、P′,过P、P′作圆心为Q的圆,使椭圆上的其余点均在圆Q外.求△PP'Q的面积S的最大值,并写出对应的圆Q的标准方程.
分析:(Ⅰ)设椭圆方程为
+
=1(a>b>0),将左焦点横坐标代入椭圆方程可得y=±
,则
=2①,又
=
②,a2=b2+c2③,联立①②③可求得a,b;
(Ⅱ)设Q(t,0)(t>0),圆的半径为r,直线PP′方程为:x=m(m>t),则圆Q的方程为:(x-t)2+y2=r2,联立圆与椭圆方程消掉y得x的二次方程,则△=0①,易求P点坐标,代入圆的方程得等式②,由①②消掉r得m=2t,则S△PP′Q=
|PP′|(m-t),变为关于t的函数,利用基本不等式可求其最大值及此时t值,由对称性可得圆心Q在y轴左侧的情况;
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a |
| b2 |
| a |
| c |
| a |
| ||
| 2 |
(Ⅱ)设Q(t,0)(t>0),圆的半径为r,直线PP′方程为:x=m(m>t),则圆Q的方程为:(x-t)2+y2=r2,联立圆与椭圆方程消掉y得x的二次方程,则△=0①,易求P点坐标,代入圆的方程得等式②,由①②消掉r得m=2t,则S△PP′Q=
| 1 |
| 2 |
解答:解:(Ⅰ)设椭圆方程为
+
=1(a>b>0),
左焦点F1(-c,0),将横坐标-c代入椭圆方程,得y=±
,
所以
=2①,
=
②,a2=b2+c2③,联立①②③解得a=4,b=2
,
所以椭圆方程为:
+
=1;
(Ⅱ)设Q(t,0)(t>0),圆的半径为r,直线PP′方程为:x=m(m>t),
则圆Q的方程为:(x-t)2+y2=r2,
由
得x2-4tx+2t2+16-2r2=0,
由△=0,即16t2-4(2t2+16-2r2)=0,得t2+r2=8,①
把x=m代入
+
=1,得y2=8(1-
)=8-
,
所以点P坐标为(m,
),代入(x-t)2+y2=r2,得(m-t)2+8-
=r2,②
由①②消掉r2得4t2-4mt+m2=0,即m=2t,
S△PP′Q=
|PP′|(m-t)=
×(m-t)=
×t=
≤
×
=2
,
当且仅当4-t2=t2即t=
时取等号,
此时t+r=
+
<4,椭圆上除P、P′外的点在圆Q外,
所以△PP'Q的面积S的最大值为2
,圆Q的标准方程为:(x-
)2+y2=6.
当圆心Q、直线PP′在y轴左侧时,由对称性可得圆Q的方程为(x+
)2+y2=6,△PP'Q的面积S的最大值仍为为2
.
| x2 |
| a2 |
| y2 |
| b2 |
左焦点F1(-c,0),将横坐标-c代入椭圆方程,得y=±
| b2 |
| a |
所以
| b2 |
| a |
| c |
| a |
| ||
| 2 |
| 2 |
所以椭圆方程为:
| x2 |
| 16 |
| y2 |
| 8 |
(Ⅱ)设Q(t,0)(t>0),圆的半径为r,直线PP′方程为:x=m(m>t),
则圆Q的方程为:(x-t)2+y2=r2,
由
|
由△=0,即16t2-4(2t2+16-2r2)=0,得t2+r2=8,①
把x=m代入
| x2 |
| 16 |
| y2 |
| 8 |
| m2 |
| 16 |
| m2 |
| 2 |
所以点P坐标为(m,
8-
|
| m2 |
| 2 |
由①②消掉r2得4t2-4mt+m2=0,即m=2t,
S△PP′Q=
| 1 |
| 2 |
8-
|
| 8-2t2 |
| 2(4-t2)t2 |
| 2 |
| (4-t2)+t2 |
| 2 |
| 2 |
当且仅当4-t2=t2即t=
| 2 |
此时t+r=
| 2 |
| 6 |
所以△PP'Q的面积S的最大值为2
| 2 |
| 2 |
当圆心Q、直线PP′在y轴左侧时,由对称性可得圆Q的方程为(x+
| 2 |
| 2 |
点评:本题考查圆、椭圆的标准方程,考查椭圆的几何性质,考查方程组的解法,考查学生的计算能力,难度较大.

练习册系列答案
相关题目
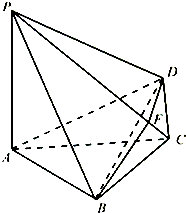 (2013•重庆)如图,四棱锥P-ABCD中,PA⊥底面ABCD,
(2013•重庆)如图,四棱锥P-ABCD中,PA⊥底面ABCD,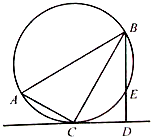 (2013•重庆)如图,在△ABC中,∠C=90°,∠A=60°,AB=20,过C作△ABC的外接圆的切线CD,BD⊥CD,BD与外接圆交于点E,则DE的长为
(2013•重庆)如图,在△ABC中,∠C=90°,∠A=60°,AB=20,过C作△ABC的外接圆的切线CD,BD⊥CD,BD与外接圆交于点E,则DE的长为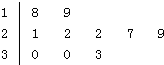 (2013•重庆)如图是某公司10个销售店某月销售某产品数量(单位:台)的茎叶图,则数据落在区间[22,30)内的概率为( )
(2013•重庆)如图是某公司10个销售店某月销售某产品数量(单位:台)的茎叶图,则数据落在区间[22,30)内的概率为( )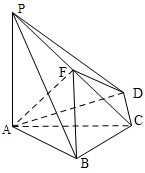 (2013•重庆)如图,四棱锥P-ABCD中,PA⊥底面ABCD,BC=CD=2,AC=4,∠ACB=∠ACD=
(2013•重庆)如图,四棱锥P-ABCD中,PA⊥底面ABCD,BC=CD=2,AC=4,∠ACB=∠ACD=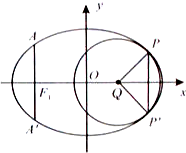 (2013•重庆)如图,椭圆的中心为原点O,长轴在x轴上,离心率
(2013•重庆)如图,椭圆的中心为原点O,长轴在x轴上,离心率