题目内容
已知数列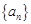 的前
的前 项和为
项和为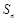 ,
,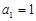 ,
, 是
是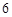 与
与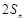 的等差中项(
的等差中项(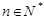 ).
).
(1)求数列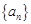 的通项公式;
的通项公式;
(2)是否存在正整数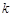 ,使不等式
,使不等式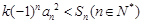 恒成立,若存在,求出
恒成立,若存在,求出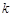
的最大值;若不存在,请说明理由.
(1)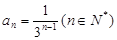 (2)存在,11
(2)存在,11
解析试题分析:
(1)解法一:根据 是
是 与
与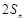 的等差中项,利用等差中项得到
的等差中项,利用等差中项得到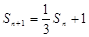 ,(
,(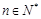 )①,
)①,
当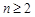 时有
时有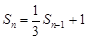 ②,则①-②可得
②,则①-②可得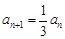 ,从而可得数列通项.
,从而可得数列通项.
解法二:根据 是
是 与
与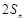 的等差中项,利用等差中项得到
的等差中项,利用等差中项得到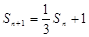 ,(
,(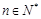 )①,根据该式的结构特征,利用构造法,可构造出等比数列
)①,根据该式的结构特征,利用构造法,可构造出等比数列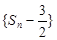 ,从而求得
,从而求得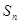 ,进而利用
,进而利用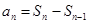 得到数列的通项.
得到数列的通项.
(2)根据(1)的结论可知,数列是等比数列,所以可以得到其前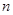 项和;代入
项和;代入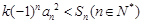 化简,讨论
化简,讨论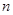 的奇偶发现,
的奇偶发现, 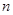 为奇数时,恒成立;
为奇数时,恒成立; 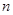 为偶数时,可将其转化为二次函数在固定区间恒成立问题,利用单调性可判断是否存在这样的正整数
为偶数时,可将其转化为二次函数在固定区间恒成立问题,利用单调性可判断是否存在这样的正整数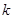 .
.
试题解析:(1)解法一:因为 是
是 与
与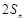 的等差中项,
的等差中项,
所以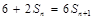 (
(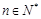 ),即
),即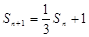 ,(
,(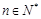 )①
)①
当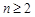 时有
时有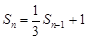 ②
②
①-②得 ,即
,即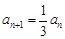 对
对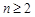 都成立
都成立
又根据①有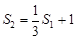 即
即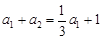 ,所以
,所以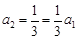
所以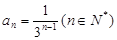 . 所以数列
. 所以数列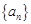 是首项为1,公比为
是首项为1,公比为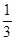 的等比数列.
的等比数列.
解法二: 因为 是
是 与
与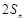 的等差中项,
的等差中项,
所以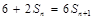 (
(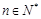 ),即
),即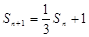 ,(
,(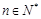 )
)
由此得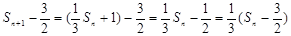 (
(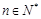 ),
),
又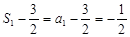 ,所以
,所以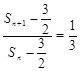 (
(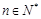 ),
),
所以数列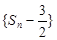 是以
是以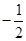 为首项,
为首项,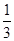 为公比的等比数列.
为公比的等比数列.
得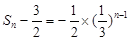 ,即
,即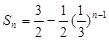 (
(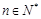 ),
),
所以,当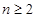 时,
时,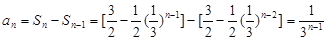 ,
,
又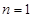 时,
时,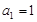 也适合上式,所以
也适合上式,所以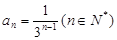 .
.
(2)根据(1)的结论可知,
数列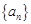 是首项为1,公比为
是首项为1,公比为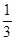 的等比数列,
的等比数列,
所以

练习册系列答案
相关题目
 }、{
}、{ 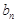 }满足:
}满足: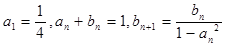 .
.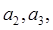
 }为等差数列,并求数列
}为等差数列,并求数列 和{
和{ 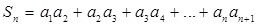 ,求实数
,求实数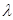 为何值时
为何值时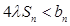 恒成立.
恒成立. 是数列
是数列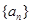 的前
的前 项和,且
项和,且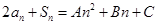 .
.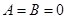 ,
,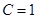 时,求
时,求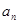 ;
; 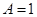 ,
,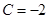 .
.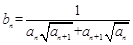 ,且数列
,且数列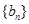 的前
的前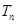 ,求
,求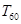 的值.
的值. 的前
的前 项和
项和 ,数列
,数列 满足
满足 .
.
 ,数列
,数列 的前
的前 ,求满足
,求满足 的
的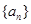 的前
的前 项和为
项和为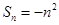 ,数列
,数列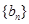 满足:
满足: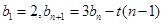 ,已知
,已知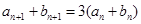 对任意
对任意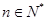 都成立
都成立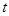 的值
的值 的前
的前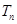 ,问是否存在互不相等的正整数
,问是否存在互不相等的正整数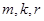 ,使得
,使得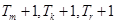 成等比数列?若存在,求出
成等比数列?若存在,求出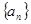 中,
中,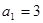 ,其前
,其前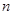 项和为
项和为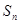 ,等比数列
,等比数列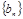 的各项均为正数,
的各项均为正数,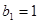 ,公比为
,公比为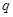 ,且
,且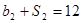 ,
,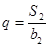 .
.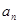 与
与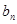 ; (2)设数列
; (2)设数列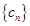 满足
满足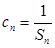 ,求
,求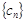 的前
的前 .
.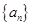 是一个公差大于0的等差数列,且满足
是一个公差大于0的等差数列,且满足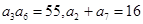 .
.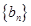 满足等式:
满足等式: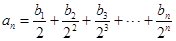 (n为正整数)求数列
(n为正整数)求数列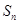 .
.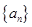 是等差数列,满足
是等差数列,满足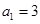 ,
, ,数列
,数列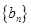 满足
满足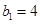 ,
,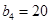 ,且
,且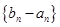 是等比数列.
是等比数列.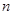 项和.
项和.