题目内容
已知数列 的前
的前 项和
项和 ,数列
,数列 满足
满足 .
.
(1)求
(2)求证数列 是等差数列,并求数列
是等差数列,并求数列 的通项公式;
的通项公式;
(3)设 ,数列
,数列 的前
的前 项和为
项和为 ,求满足
,求满足 的
的 的最大值.
的最大值.
(1) ;(2)证明详见解析,
;(2)证明详见解析,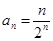 ;(3)
;(3) 的最大值为
的最大值为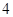 .
.
解析试题分析:(1)根据条件中 ,可令
,可令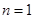 ,结合
,结合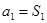 ,即可得:
,即可得: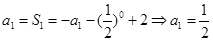 ;(2)欲证
;(2)欲证 是等差数列,而条件中
是等差数列,而条件中 ,因此可以首先根据数列
,因此可以首先根据数列 满足的条件
满足的条件 探究
探究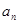 与
与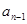 满足的关系,进而可以得到数列
满足的关系,进而可以得到数列 中
中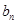 与
与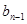 满足的关系:当
满足的关系:当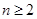 时,
时,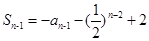 ,
,
∴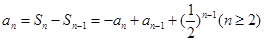 ,即
,即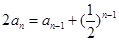 ,∴
,∴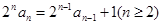 ,
,
又∵  ,∴
,∴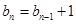 ,而
,而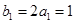 ,∴
,∴ 是以
是以 为首项,
为首项, 为公差的等差数列,
为公差的等差数列,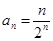 ;
;
(3)由(2)结合条件 ,可得
,可得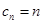 ,因此可以考虑采用裂项相消法求数列
,因此可以考虑采用裂项相消法求数列 的前
的前 项和
项和 :
: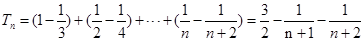 ,从而可将
,从而可将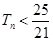 转化为关于
转化为关于 的不等式:
的不等式: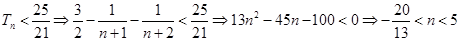 ,结合
,结合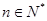 ,即可知
,即可知 的最大值为
的最大值为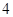 .
.
试题解析:(1)∵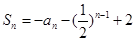 ,∴令n=1,
,∴令n=1,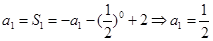 ;
;
(2)证明:在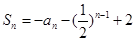 中,当
中,当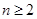 时,
时,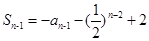 ,
,
∴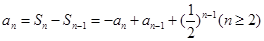 ,即
,即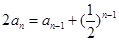 ,∴
,∴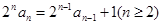 ,
,
又∵  ,∴
,∴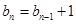 ,而
,而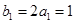 ,∴
,∴ 是以
是以 为首项,
为首项, 为公差的等差数列,
为公差的等差数列,
∴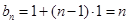 ,∴
,∴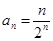 ;
;
(3)由(2)及 ,∴
,∴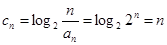 cn=log2=log22n=n,
cn=log2=log22n=n,
∴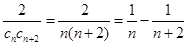 ,∴
,∴ 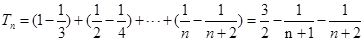 ,
,
∴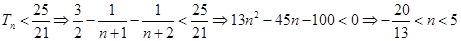 ,
,
又∵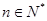 ,∴
,∴ 的最大值为
的最大值为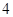 .
.
考点:1.等差数列的证明;2.求数列的通项公式;3.裂项相消法求数列的和.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
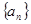 的前三项为
的前三项为 ,则此数列的通项公式为______ .
,则此数列的通项公式为______ .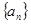 满足:
满足: ,
,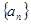 的前
的前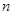 项和为
项和为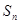 .
.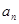 及
及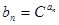 (其中
(其中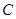 为常数,且
为常数,且 ),求证数列
),求证数列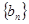 为等比数列.
为等比数列.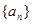 的前
的前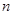 项和为
项和为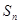 ,
, ,
,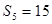 ,
,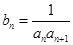 ,求数列
,求数列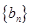 的前100项和.
的前100项和. 的前
的前 项和为
项和为 ,对一切
,对一切 ,点
,点 都在函数
都在函数 的图象上
的图象上 归纳数列
归纳数列 ),
), ,
, ,
, ;
; ,
, ,
, ,
, ;
; ,…..,
,….., ,
, 的值;
的值;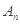 为数列
为数列 的前
的前 对一切
对一切 ,求
,求 的取值范围
的取值范围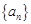 的前
的前 项和为
项和为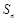 ,
,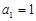 ,
, 是
是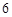 与
与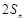 的等差中项(
的等差中项(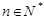 ).
).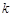 ,使不等式
,使不等式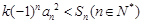 恒成立,若存在,求出
恒成立,若存在,求出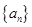 的前
的前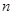 项和为
项和为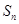 ,
,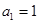 ,
,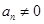 ,
,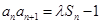 ,其中
,其中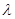 为常数,
为常数,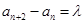 ;
;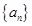 的前
的前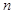 项和记为
项和记为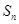 ,
, ,
,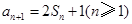 .
.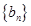 的各项为正,其前
的各项为正,其前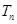 ,且
,且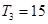 ,又
,又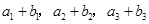 成等比数列,求
成等比数列,求