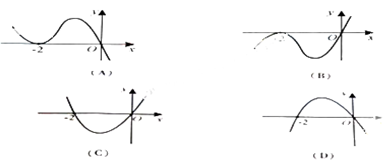题目内容
已知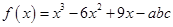 ,
,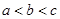 ,且
,且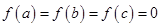 .现给出如下结论:
.现给出如下结论:
①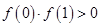 ;②
;②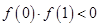 ;③
;③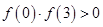 ;④
;④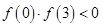 .
.
其中正确结论的序号是( )
| A.①③ | B.①④ | C.②③ | D.②④ |
C
解析试题分析: ,
, ,结合导数可知,函数
,结合导数可知,函数 在区间
在区间 上单调递增,在区间
上单调递增,在区间 上单调递减,在区间
上单调递减,在区间 上单调递增,因此函数
上单调递增,因此函数 在
在 处取得极大值,在
处取得极大值,在 处取得极小值,由于
处取得极小值,由于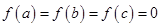 ,且
,且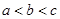 ,结合三次函数图象可知,
,结合三次函数图象可知, ,
, ,
, ,因此
,因此 ,所以
,所以 ,
, ,
,
由于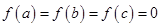 ,且
,且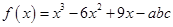 ,则
,则
 ,因此
,因此 ,
, ,下面来说明
,下面来说明 ,
,
由于 ,
, ,
, ,由基本不等式得
,由基本不等式得 ,
,
于是有 ,即
,即 ,整理得
,整理得 ,解得
,解得 ,
,
因此 ,所以
,所以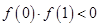 ,
,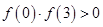 .故选C.
.故选C.
考点:1.导数;2.根与方程的系数的关系;3.基本不等式

练习册系列答案
相关题目
已知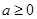 ,函数
,函数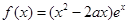 ,若
,若 在
在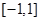 上是单调减函数,则
上是单调减函数,则 的取值范围是( )
的取值范围是( )
A.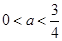 | B.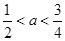 | C.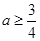 | D.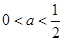 |
设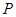 为曲线
为曲线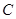 :
: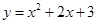 上的点,且曲线
上的点,且曲线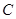 在点
在点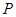 处切线倾斜角的取值范围为
处切线倾斜角的取值范围为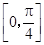 ,则点
,则点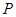 横坐标的取值范围为
横坐标的取值范围为
A.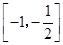 | B.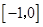 | C.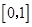 | D.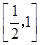 |
设点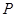 在曲线
在曲线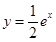 上,点
上,点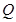 在曲线
在曲线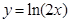 上,则
上,则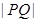 的最小值为( )
的最小值为( )
A.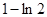 | B.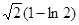 | C.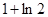 | D.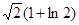 |
设函数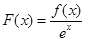 是定义在
是定义在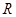 上的函数,其中
上的函数,其中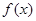 的导函数为
的导函数为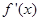 ,满足
,满足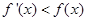 对于
对于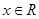 恒成立,则
恒成立,则
A.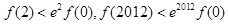 | B.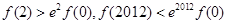 |
C.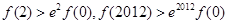 | D.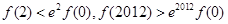 |
若 ,则
,则 ( )
( )
A. | B. | C. | D. |
曲线y=e-2x+1在点(0,2)处的切线与直线y=0和y=x围成的
三角形的面积为 ( ).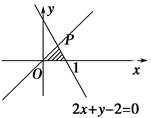
A.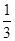 | B.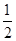 | C.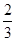 | D.1 |
设f0(x)=cos x,f1(x)=f0′(x),f2(x)=f1′(x),…,fn+1(x)=fn′(x),n∈
N,则f2 011(x)等于 ( ).
| A.sin x | B.-sin x |
| C.cos x | D.-cos x |
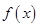 在R上可导,其导函数
在R上可导,其导函数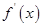 ,且函数
,且函数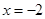 处取得极小值,则函数
处取得极小值,则函数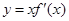 的图像可能是( )
的图像可能是( )