题目内容
设函数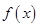 在R上可导,其导函数
在R上可导,其导函数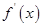 ,且函数
,且函数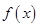 在
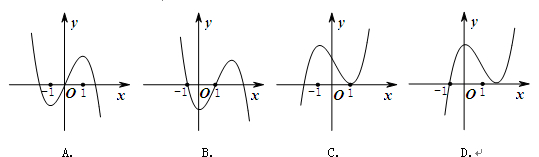
在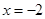 处取得极小值,则函数
处取得极小值,则函数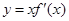 的图像可能是( )
的图像可能是( )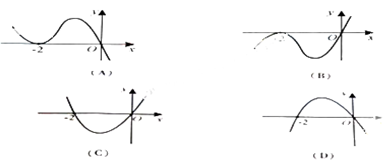
C
解析试题分析:∵函数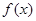 在
在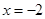 处取得极小值,∴
处取得极小值,∴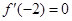 ,且函数
,且函数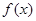 在
在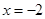 左侧附近为减函数,在
左侧附近为减函数,在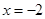 右侧附近为增函数,即当
右侧附近为增函数,即当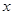 在
在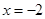 左侧附近时,
左侧附近时,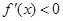 ,当
,当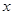 在
在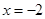 右侧附近时,
右侧附近时,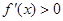 ,从而当
,从而当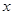 在
在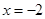 左侧附近时,
左侧附近时,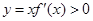 ,当
,当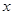 在
在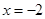 右侧附近且
右侧附近且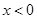 时,
时,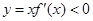 ,观察各选项可知只有C符合题意,故选C.
,观察各选项可知只有C符合题意,故选C.
考点:1.函数的极值与导数;2.函数的单调性与导数.

练习册系列答案
相关题目
设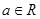 ,函数
,函数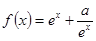 的导函数
的导函数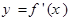 是奇函数,若曲线
是奇函数,若曲线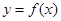 的一条切线的斜率为
的一条切线的斜率为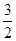 ,则切点的横坐标是( )
,则切点的横坐标是( )
A.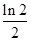 | B. | C.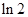 | D.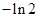 |
设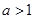 ,若曲线
,若曲线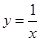 与直线
与直线 ,
,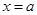 ,
,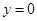 所围成封闭图形的面积为2,则
所围成封闭图形的面积为2,则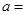 ( )
( )
| A.2 | B.e | C.2e | D.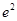 |
已知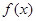 为
为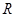 上的可导函数,且
上的可导函数,且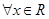 ,均有
,均有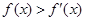 ,则以下判断正确的是
,则以下判断正确的是
A.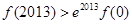 | B.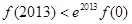 |
C.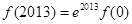 | D.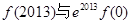 大小无法确定 大小无法确定 |
已知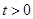 ,若
,若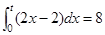 ,则
,则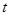 = ( )
= ( )
| A.1 | B.-2 | C.-2或4 | D.4 |
设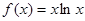 ,若
,若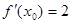 ,则
,则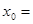 ( )
( )
A.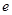 | B.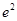 | C.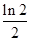 | D.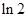 |
已知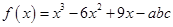 ,
,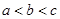 ,且
,且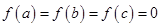 .现给出如下结论:
.现给出如下结论:
①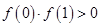 ;②
;②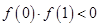 ;③
;③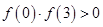 ;④
;④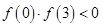 .
.
其中正确结论的序号是( )
| A.①③ | B.①④ | C.②③ | D.②④ |
函数y=xcos x-sin x在下面哪个区间内是增函数 ( ).
A.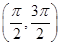 | B.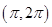 | C.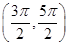 | D.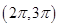 |
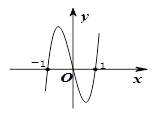
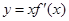 的图象如图所示(其中
的图象如图所示(其中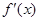 是函数
是函数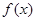 的导函数).下面四个图象中,
的导函数).下面四个图象中,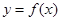 的图象大致是( )
的图象大致是( )