题目内容
在R上定义运算?:x?y=(1-x)(1-y).若不等式(x-a)?(x+a)>-1对任意实数x成立,则( )
| A.-1<a<1 | B.-2<a<0 | C.0<a<2 | D.-
|
根据题中已知的新定义得:
(x-a)?(x+a)=[1-(x-a)][1-(x+a)]=(x-a-1)(x+a-1),
因为(x-a)?(x+a)>-1,
所以可得不等式(x-a-1)(x+a-1)>-1,整理可得:x2-2x+2-a2>0,
∵不等式对于任意实数x都成立,
∴△=4-4(2-a2)<0,
解得:-1<a<1,
则实数a的取值范围是(-1,1).
故选A.
(x-a)?(x+a)=[1-(x-a)][1-(x+a)]=(x-a-1)(x+a-1),
因为(x-a)?(x+a)>-1,
所以可得不等式(x-a-1)(x+a-1)>-1,整理可得:x2-2x+2-a2>0,
∵不等式对于任意实数x都成立,
∴△=4-4(2-a2)<0,
解得:-1<a<1,
则实数a的取值范围是(-1,1).
故选A.

练习册系列答案
相关题目
 :x
:x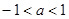 B.0<
B.0< <2 C.
<2 C. D.
D.
 :x
:x B.
B. C.
C. D.
D.