题目内容
集合A={x|x2-2x≤0}，B={x|lg（x-1）≤0}，则A∩B=（ ）
| A、{x|1≤x≤2} |
| B、{x|1＜x≤2} |
| C、{x|-1＜x＜0} |
| D、{x|x≤2} |
考点：指、对数不等式的解法,交集及其运算,一元二次不等式的解法
专题：计算题,不等式的解法及应用
分析：求解二次不等式得到集合A，求解对数不等式得到集合B，然后求解交集．
解答：
解：A={x|x2-2x≤0}={x|0≤x≤2}，
B={x|lg（x-1）≤0}={x|0＜x-1≤1}={x|1＜x≤2}，
所以A∩B={x|1＜x≤2}，
故选：B．
B={x|lg（x-1）≤0}={x|0＜x-1≤1}={x|1＜x≤2}，
所以A∩B={x|1＜x≤2}，
故选：B．
点评：本题考查集合交集的求法，绝对值不等式的解法以及二次不等式的解法，考查计算能力．
练习册系列答案
相关题目
设A（3，2，1），B（1，0，5），C（0，2，1），AB的中点为M，则|CM|=（ ）
| A、3 | ||
B、
| ||
C、2
| ||
D、3
|
不等式x-2y+5＞0表示的区域在直线x-2y+5=0的（ ）
| A、右上方 | B、右下方 |
| C、左上方 | D、左下方 |
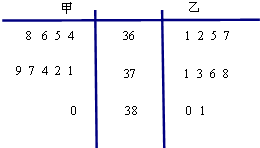学校为了预防甲流感，每天上午都要对同学进行体温抽查．某一天，随机抽取甲、乙两个班级各10名同学，测量他们的体温如图：（单位0.1℃）