题目内容
(本小题满分14分)
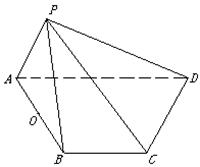
如图, 在四棱锥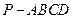 中,顶点
中,顶点 在底面
在底面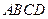 上的射影恰好落在
上的射影恰好落在 的中点
的中点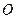 上,又∠
上,又∠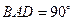 ,
,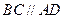 ,且
,且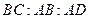
=1:2:2.
(1) 求证: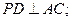
(2) 若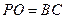 , 求直线
, 求直线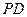 与
与 所成的角的余弦值;
所成的角的余弦值;
(3) 若平面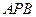 与平面
与平面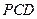 所成的角为
所成的角为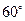 , 求
, 求 的值
的值
如图, 在四棱锥
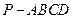 中,顶点
中,顶点 在底面
在底面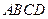 上的射影恰好落在
上的射影恰好落在 的中点
的中点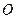 上,又∠
上,又∠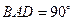 ,
,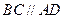 ,且
,且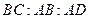
=1:2:2.

(1) 求证:
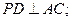
(2) 若
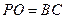 , 求直线
, 求直线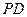 与
与 所成的角的余弦值;
所成的角的余弦值;(3) 若平面
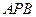 与平面
与平面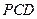 所成的角为
所成的角为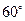 , 求
, 求 的值
的值(1)证明略
(2)
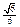
(3)
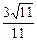
因为 中点
中点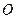 为点
为点 在平面ABCD内的射影, 所以
在平面ABCD内的射影, 所以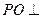 底面
底面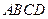 . 以
. 以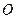 为坐标原点,
为坐标原点,  所在直线为
所在直线为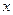 轴,
轴, 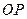 所在直线为
所在直线为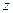 轴, 建立空间直角坐标系
轴, 建立空间直角坐标系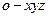
(如图).
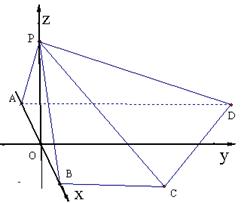
(1)设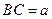 , OP = h则依题意得:
, OP = h则依题意得:
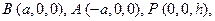
--- 4分
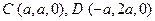 .
.
∴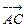 =
= 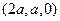 ,
, 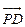 =
= 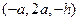 ,
,
于是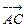 ·
·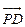 =
= 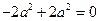 , ∴
, ∴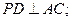
(2)由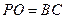 , 得h =" a," 于是
, 得h =" a," 于是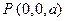 ,
,
--- 5分
∵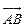 =
= 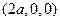 ,
, 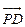 =
= 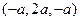 , ∴
, ∴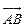 ·
·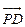 =
= 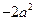 ,
,
cos<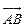 ,
,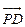 > =
> = 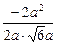 =
=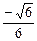 , ∴ 直线
, ∴ 直线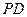 与
与 所成的角的余弦值为
所成的角的余弦值为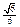 ;
;
(3) 设平面 的法向量为m, 可得m =" (0,1,0" ),
的法向量为m, 可得m =" (0,1,0" ),
设平面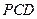 的法向量为n =
的法向量为n = 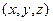 , 由
, 由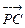 =
= 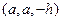 ,
, 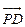 =
= 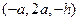 ,
,
∴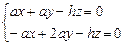 , 解得n =" (1," 2 ,
, 解得n =" (1," 2 ,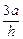 ), ∴ m•n =" 2" ,
), ∴ m•n =" 2" ,
cos< m, n > =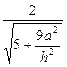 , ∵ 二面角为
, ∵ 二面角为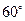 , ∴
, ∴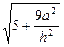 = 4,
= 4,
解得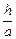 =
=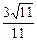 ,即
,即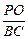 =
=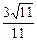 . --- 5分
. --- 5分
(以传统方法解答相应给分)
 中点
中点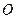 为点
为点 在平面ABCD内的射影, 所以
在平面ABCD内的射影, 所以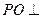 底面
底面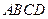 . 以
. 以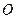 为坐标原点,
为坐标原点,  所在直线为
所在直线为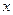 轴,
轴, 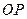 所在直线为
所在直线为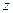 轴, 建立空间直角坐标系
轴, 建立空间直角坐标系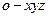
(如图).

(1)设
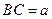 , OP = h则依题意得:
, OP = h则依题意得: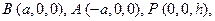
--- 4分
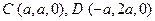 .
. ∴
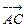 =
= 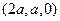 ,
, 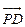 =
= 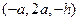 ,
, 于是
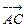 ·
·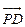 =
= 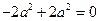 , ∴
, ∴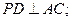
(2)由
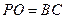 , 得h =" a," 于是
, 得h =" a," 于是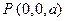 ,
, --- 5分
∵
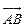 =
= 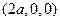 ,
, 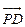 =
= 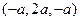 , ∴
, ∴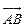 ·
·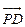 =
= 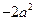 ,
, cos<
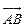 ,
,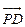 > =
> = 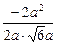 =
=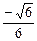 , ∴ 直线
, ∴ 直线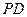 与
与 所成的角的余弦值为
所成的角的余弦值为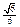 ;
;(3) 设平面
 的法向量为m, 可得m =" (0,1,0" ),
的法向量为m, 可得m =" (0,1,0" ),设平面
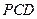 的法向量为n =
的法向量为n = 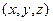 , 由
, 由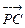 =
= 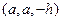 ,
, 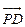 =
= 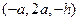 ,
, ∴
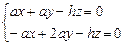 , 解得n =" (1," 2 ,
, 解得n =" (1," 2 ,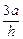 ), ∴ m•n =" 2" ,
), ∴ m•n =" 2" ,cos< m, n > =
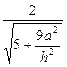 , ∵ 二面角为
, ∵ 二面角为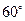 , ∴
, ∴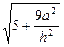 = 4,
= 4,解得
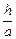 =
=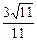 ,即
,即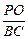 =
=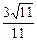 . --- 5分
. --- 5分(以传统方法解答相应给分)

练习册系列答案
相关题目
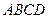 、
、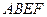 的边长都是1,平面
的边长都是1,平面 平面
平面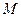 在
在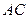 上移动,点
上移动,点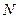 在
在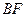 上移动,若
上移动,若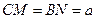 (
(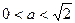 )
)
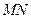 的长;
的长;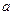 为何值时,
为何值时,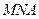 与面
与面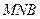 所成锐二面角余弦值的大小.
所成锐二面角余弦值的大小.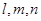 是三条不重合的直线,
是三条不重合的直线, 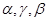 是三个不重合的平面,下列四个命题正确的个数为 ( )
是三个不重合的平面,下列四个命题正确的个数为 ( )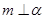 , m∥
, m∥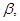
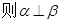
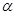 所成的角相等,则m∥n;
所成的角相等,则m∥n;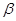 ,n∥β,则
,n∥β,则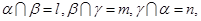
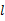 ∥
∥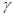 ,则m∥n.
,则m∥n. 中,
中,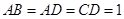 ,
, 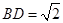 ,
,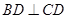 .将四边形
.将四边形 折成四面体
折成四面体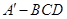 ,使平面
,使平面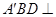 平面
平面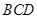 ,则下列结论正确的是
,则下列结论正确的是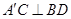
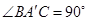
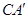 与平面
与平面 所成的角为
所成的角为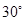
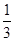
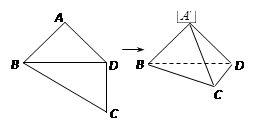
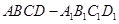 中,
中,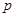 是侧面
是侧面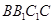 内一动点,若
内一动点,若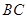 与直线
与直线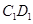 的距离相等,则动点
的距离相等,则动点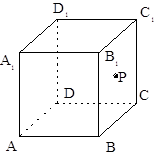
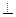 平面ABCD,四边形ABEF与ABCD都是直角梯形,
平面ABCD,四边形ABEF与ABCD都是直角梯形,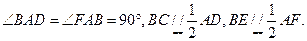

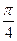 .
.  视图中大三角形的边长是2的正三角形,俯视图为正六边形,那么该几何体的体积为 .
视图中大三角形的边长是2的正三角形,俯视图为正六边形,那么该几何体的体积为 .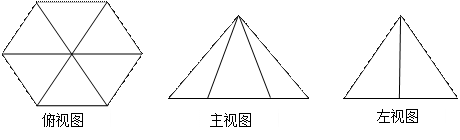
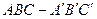 的
的 底面是边长为1cm的正三角形,侧面是长方形,侧棱长为4cm,一个小虫从A点出发沿表面一圈到达
底面是边长为1cm的正三角形,侧面是长方形,侧棱长为4cm,一个小虫从A点出发沿表面一圈到达 点,则小虫所行的最短路程为__________cm
点,则小虫所行的最短路程为__________cm