题目内容
(12分)
已知四棱锥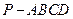 中,
中,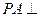 平面
平面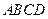 ,底面
,底面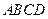
 是直角梯形,
是直角梯形,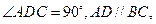
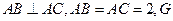 为
为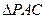
 的重心,
的重心,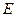 为
为 的中点,
的中点,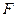 在
在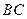 上,且
上,且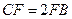 ;
;

(1)求证: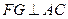 ;
;
(2)当
 二面角
二面角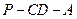 的正切值为多少时,
的正切值为多少时,
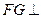 平面
平面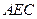 ;
;
(3)在(2)的条件下,求直线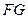 与平面
与平面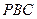 所
所 成角
成角
的正弦值;
已知四棱锥
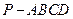 中,
中,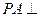 平面
平面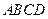 ,底面
,底面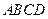
 是直角梯形,
是直角梯形,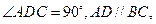
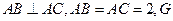 为
为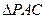
 的重心,
的重心,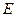 为
为 的中点,
的中点,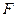 在
在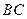 上,且
上,且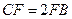 ;
;
(1)求证:
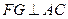 ;
;(2)当

 二面角
二面角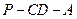 的正切值为多少时,
的正切值为多少时,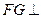 平面
平面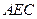 ;
;(3)在(2)的条件下,求直线
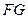 与平面
与平面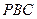 所
所 成角
成角的正弦值;
(1)略
(2) 当二面角P-CD-A的正切值为2时,FG⊥平面AEC
(3)
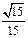
(1)连结CG并延长交PA于H,连结BH
∵G是△PAC的重心 ∴CG:GH="2:1 "
∵CF:FB="2:1 " ∴CG:GH=CF:FB ∴FG∥BH
∴FG∥BH
∵PA⊥平面ABCD ∴PA⊥AC ∴AC⊥平面PAB
∴ AC⊥BH ∵FG∥BH ∴FG⊥AC ----------
---------- --4分
--4分
(2)如图所示,以A为坐标原点建立空间直角坐标系

∵A B=AC=2且AB⊥AC ∴∠A
B=AC=2且AB⊥AC ∴∠A CB=45° 在直角梯形ABCD中
CB=45° 在直角梯形ABCD中
∵∠BCD= 9
9 0° ∴∠ACD=45°∵AC="2 " ∴AD=CD=
0° ∴∠ACD=45°∵AC="2 " ∴AD=CD=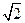
∵PA⊥平面ABCD ∴PA⊥CD ∵CD ⊥AD ∴CD⊥平面PAD
⊥AD ∴CD⊥平面PAD
∴CD⊥PD ∴∠PDA为二面角P-CD-A的平面 角
角
∴A(0,0,0) C(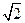 ,
,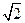 ,0) D(0,
,0) D(0,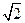 ,0) B(
,0) B(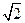 ,
,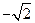 ,0)
,0)
设P(0,0,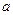 ) ∴
) ∴ H(0,0,
H(0,0,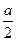 ) E(
) E(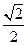 ,
,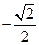 ,
,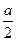 )
)
∵FG⊥平面AEC ∴FG⊥AE∵FG∥BH ∴BH⊥AE
∴BH⊥AE
∴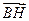 =(
=(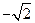 ,
,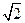 ,
,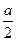 )
) 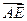 =(
=(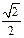 ,
, ,
,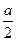 )
)
∴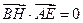 ∴
∴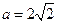
 ∴PA=
∴PA=
∴ ∠PDA="2 " ∴当二面角P-CD-A的正切值为2时,FG⊥平面AEC ------8分
∠PDA="2 " ∴当二面角P-CD-A的正切值为2时,FG⊥平面AEC ------8分
(3)∵BH∥FG ∴FG与平面PBC所成的角等于BH与平面PBC所成的角
∵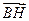 =(
=(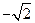 ,
,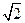 ,
,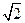 )
) 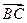 =(0,
=(0, ,0)
,0) 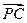 =(
=(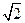 ,
,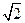 ,
,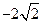 )
)
设平面PBC的法向量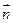 =(x,y,z
=(x,y,z ) ∴
) ∴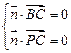 ∴
∴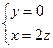 令z="1 " ∴
令z="1 " ∴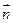 =(2,0,1)
=(2,0,1)
∴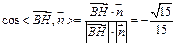 设直线FG与平面PB
设直线FG与平面PB C所成的角为
C所成的角为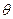
∴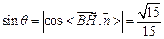 ∴直线FG与平面PBC所成的角的正弦值为
∴直线FG与平面PBC所成的角的正弦值为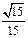 --12分
--12分
∵G是△PAC的重心 ∴CG:GH="2:1 "
∵CF:FB="2:1 " ∴CG:GH=CF:FB
 ∴FG∥BH
∴FG∥BH∵PA⊥平面ABCD ∴PA⊥AC ∴AC⊥平面PAB
∴ AC⊥BH ∵FG∥BH ∴FG⊥AC
 ----------
---------- --4分
--4分(2)如图所示,以A为坐标原点建立空间直角坐标系

∵A
 B=AC=2且AB⊥AC ∴∠A
B=AC=2且AB⊥AC ∴∠A CB=45° 在直角梯形ABCD中
CB=45° 在直角梯形ABCD中 ∵∠BCD=
 9
9 0° ∴∠ACD=45°∵AC="2 " ∴AD=CD=
0° ∴∠ACD=45°∵AC="2 " ∴AD=CD=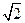
∵PA⊥平面ABCD ∴PA⊥CD ∵CD
 ⊥AD ∴CD⊥平面PAD
⊥AD ∴CD⊥平面PAD∴CD⊥PD ∴∠PDA为二面角P-CD-A的平面
 角
角∴A(0,0,0) C(
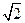 ,
,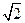 ,0) D(0,
,0) D(0,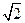 ,0) B(
,0) B(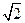 ,
,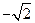 ,0)
,0)设P(0,0,
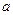 ) ∴
) ∴ H(0,0,
H(0,0,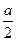 ) E(
) E(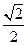 ,
,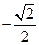 ,
,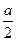 )
) ∵FG⊥平面AEC ∴FG⊥AE∵FG∥BH
 ∴BH⊥AE
∴BH⊥AE ∴
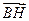 =(
=(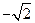 ,
,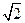 ,
,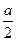 )
) 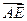 =(
=(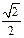 ,
, ,
,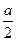 )
)
∴
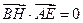 ∴
∴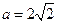
 ∴PA=
∴PA=
∴
 ∠PDA="2 " ∴当二面角P-CD-A的正切值为2时,FG⊥平面AEC ------8分
∠PDA="2 " ∴当二面角P-CD-A的正切值为2时,FG⊥平面AEC ------8分(3)∵BH∥FG ∴FG与平面PBC所成的角等于BH与平面PBC所成的角
∵
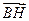 =(
=(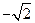 ,
,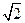 ,
,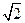 )
) 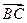 =(0,
=(0, ,0)
,0) 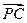 =(
=(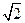 ,
,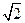 ,
,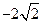 )
)设平面PBC的法向量
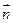 =(x,y,z
=(x,y,z ) ∴
) ∴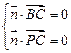 ∴
∴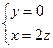 令z="1 " ∴
令z="1 " ∴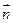 =(2,0,1)
=(2,0,1)∴
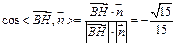 设直线FG与平面PB
设直线FG与平面PB C所成的角为
C所成的角为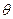
∴
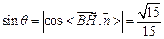 ∴直线FG与平面PBC所成的角的正弦值为
∴直线FG与平面PBC所成的角的正弦值为 --12分
--12分
练习册系列答案
相关题目
 中,棱AB=BC=3,
中,棱AB=BC=3, =4,连结
=4,连结 , 在
, 在 上有点E,使得
上有点E,使得 ⊥平面EBD ,BE交
⊥平面EBD ,BE交
 所成角的大小;
所成角的大小; 的
的 别是棱BB1、CC1、DD1的中点。
别是棱BB1、CC1、DD1的中点。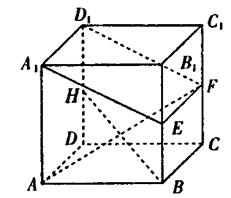
 、
、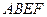 的边长都是1,平面
的边长都是1,平面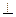 平面
平面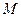 在
在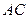 上移动,点
上移动,点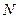 在
在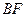 上移动,若
上移动,若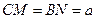 (
(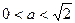 )
)
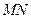 的长;
的长;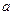 为何值时,
为何值时,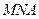 与面
与面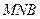 所成锐二面角余弦值的大小.
所成锐二面角余弦值的大小.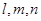 是三条不重合的直线,
是三条不重合的直线, 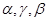 是三个不重合的平面,下列四个命题正确的个数为 ( )
是三个不重合的平面,下列四个命题正确的个数为 ( )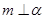 , m∥
, m∥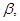
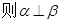
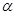 所成的角相等,则m∥n;
所成的角相等,则m∥n;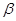 ,n∥β,则
,n∥β,则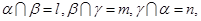
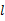 ∥
∥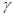 ,则m∥n.
,则m∥n.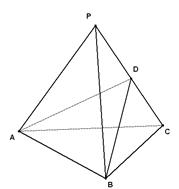
 视图中大三角形的边长是2的正三角形,俯视图为正六边形,那么该几何体的体积为 .
视图中大三角形的边长是2的正三角形,俯视图为正六边形,那么该几何体的体积为 .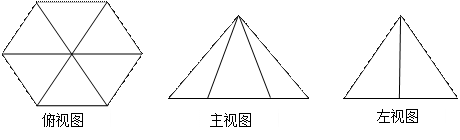
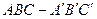 的
的 底面是边长为1cm的正三角形,侧面是长方形,侧棱长为4cm,一个小虫从A点出发沿表面一圈到达
底面是边长为1cm的正三角形,侧面是长方形,侧棱长为4cm,一个小虫从A点出发沿表面一圈到达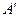 点,则小虫所行的最短路程为__________cm
点,则小虫所行的最短路程为__________cm