题目内容
已知函数 的最大值为3,最小值为
的最大值为3,最小值为 .
.
(1)求 的值;
的值;
(2)当求 时,函数
时,函数 的值域.
的值域.
(1) ;(2)函数
;(2)函数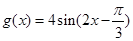 在
在 的值域为
的值域为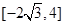 .
.
解析试题分析:(1)先由余弦函数的图像与性质及 得到函数
得到函数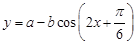 的最值,从而列出方程组
的最值,从而列出方程组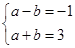 ,求解即可得到
,求解即可得到 的值;(2)将(1)求出的
的值;(2)将(1)求出的 值代入得到
值代入得到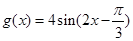 ,将
,将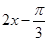 当整体,先算出
当整体,先算出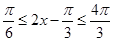 ,进而由正弦函数的图像与性质得到
,进而由正弦函数的图像与性质得到 ,进而可确定函数
,进而可确定函数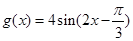 的值域.
的值域.
试题解析:(1)由余弦函数的性质可知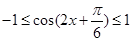 ,又
,又 ,所以
,所以 ,所以
,所以 ,所以
,所以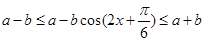
因为函数 的最大值为3,最小值为
的最大值为3,最小值为
所以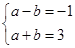 ,求解得到
,求解得到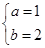
(2)由(1)可得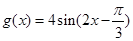
因为 ,所以
,所以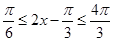 ,由正弦函数的性质可得
,由正弦函数的性质可得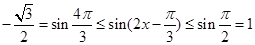 ,所以
,所以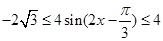
所以函数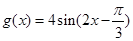 的值域为
的值域为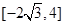 .
.
考点:1.三角函数的图像与性质;2.不等式的性质.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
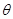 的终边过点P
的终边过点P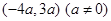 ,
,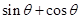 的值
的值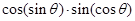 的符号
的符号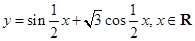 .
. .
. 的最大值,并写出
的最大值,并写出 的取值集合;
的取值集合; 中,角
中,角 的对边分别为
的对边分别为 若
若
 求实数
求实数 的最小值.
的最小值. .
. 的最小正周期和值域;
的最小正周期和值域; 中,角
中,角 的对边分别为
的对边分别为 ,若
,若 且
且 ,
, ,求
,求 和
和 .
.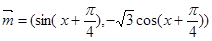 ,
, ,函数
,函数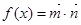 ,
, .
.
 的图像的对称中心坐标;
的图像的对称中心坐标; 个单位,再向左平移
个单位,再向左平移 个单位得函数
个单位得函数 的图像,试写出
的图像,试写出 上的图像.
上的图像.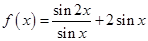 .
.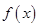 的定义域和最小正周期;
的定义域和最小正周期;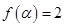 ,
,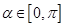 ,求
,求 的值.
的值.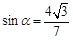 ,
,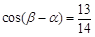 ,且
,且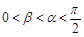 .
.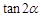 的值;
的值;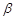 的值.
的值. =
= ,A∈
,A∈ .
. sinAsinx的值域.
sinAsinx的值域.