题目内容
要建一间地面面积为20m2，墙高为3m的长方形储藏室，在四面墙中有一面安装一扇门．已知含门一面的平均造价为300元/m2，其余三面的造价为200元/m2，屋顶的造价为250元/m2．问怎样设计储藏室地面矩形的长与宽，能使总价最低，最低造价是多少？
解：设含门的一面长为x，则总造价为
y=3x（300+200）+（
）×200×2+20×250
=1500x+
+5000≥17000
当且仅当1500x=时等号成立
所以x=4
所以含门的一面及其对面长4m，另外两面长5m
此时总价最低为17000元
答：储藏室地面矩形的长与宽分别为4m，5m，能使总价最低，最低造价是17000元
分析：总造价等于四面墙的造价加上屋顶的造价，再利用基本不等式，可求出能使总价最低的长与宽．
点评：本题以实际问题为载体，考查考生模型的构建，考查基本不等式的运用，考查学生分析解决问题的能力．
y=3x（300+200）+（
）×200×2+20×250=1500x+
+5000≥17000当且仅当1500x=
时等号成立所以x=4
所以含门的一面及其对面长4m，另外两面长5m
此时总价最低为17000元
答：储藏室地面矩形的长与宽分别为4m，5m，能使总价最低，最低造价是17000元
分析：总造价等于四面墙的造价加上屋顶的造价，再利用基本不等式，可求出能使总价最低的长与宽．
点评：本题以实际问题为载体，考查考生模型的构建，考查基本不等式的运用，考查学生分析解决问题的能力．
练习册系列答案
相关题目
某开发商对去年市场上一种商品销售数量及销售利润情况进行了调查，发现：
①销售数量y1（万件）与时间（月份）具有满足如表的一次函数关系：
| 时间x（月份） | 1 | 2 | 3 | … | 11 | 12 |
| 销售数量y1（万件） | 1.7 | 1.8 | 1.9 | … | 2.7 | 2.8 |
请根据以上信息解答下列问题：
（Ⅰ）在三月份，销售这种商品可获利润多少万元？
（Ⅱ）哪一个月的销售利润最大？请说明理由．
对任意的实数x＞0，y＞0恒成立，则实数a的最小值为________．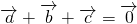
，
=3，
=5，
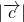=7．求
．
如图，在底面是矩形的四棱锥P-ABCD中，PA⊥平面ABCD，PA=AB=1，BC=2．
，若存在，求出BG的值；若不存在，请说明理由．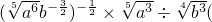
其中a＞0，b＞0）；
．
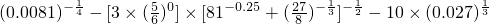的等差数列，且他参加第一次考核合格的概率大于
，他直到参加第二次考核才合格的概率为
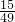．（1）求小明参加第一次考核就合格的概率；（2）求小明参加考核的次数ξ的分布列和数学期望．
（2009年）若f（1）、f（2）、f（3）、f（4）分别表示（1）、（2）、（3）、（4）各图案中圆圈的个数，按图中的规律：