题目内容
(13分)已知数列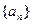 的前n项和为
的前n项和为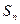 ,并且满足
,并且满足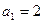 ,
,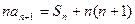 ,
,
(1)求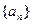 的通项公式;
的通项公式;
(2)令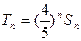 ,问是否存在正整数
,问是否存在正整数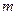 ,对一切正整数
,对一切正整数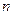 ,总有
,总有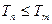 ,若存在,求
,若存在,求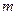 的值;若不存在,说明理由.
的值;若不存在,说明理由.
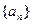 的前n项和为
的前n项和为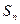 ,并且满足
,并且满足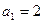 ,
,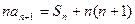 ,
,(1)求
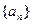 的通项公式;
的通项公式;(2)令
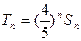 ,问是否存在正整数
,问是否存在正整数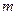 ,对一切正整数
,对一切正整数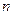 ,总有
,总有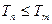 ,若存在,求
,若存在,求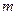 的值;若不存在,说明理由.
的值;若不存在,说明理由.解:(1)令 ,由
,由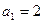 及
及 ①
①
得 ,故
,故 ,当
,当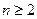 时,有
时,有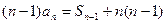 ②
②
①-②得: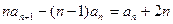
整理得,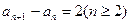
当 时,
时, ,
,
所以数列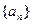 是以2为首项,以2为公差的等差数列,
是以2为首项,以2为公差的等差数列,
故 ……………………(6分)
……………………(6分)
(2)由(1)得 ,
,
所以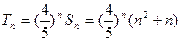 .
.
故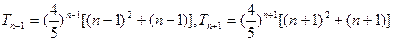 ,
,
令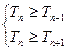 ,即
,即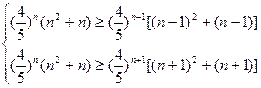
解得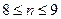 .
.
故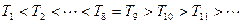
故存在正整数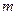 对一切正整数
对一切正整数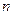 ,
,
总有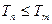 ,此时
,此时 或
或 ……………………………..(13分)
……………………………..(13分)
 ,由
,由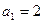 及
及 ①
①得
 ,故
,故 ,当
,当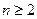 时,有
时,有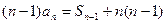 ②
②①-②得:
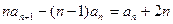
整理得,
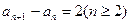
当
 时,
时, ,
,所以数列
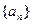 是以2为首项,以2为公差的等差数列,
是以2为首项,以2为公差的等差数列,故
 ……………………(6分)
……………………(6分)(2)由(1)得
 ,
,所以
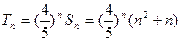 .
.故
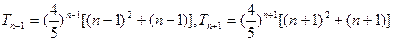 ,
,令
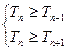 ,即
,即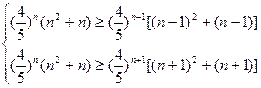
解得
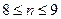 .
.故
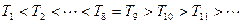
故存在正整数
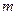 对一切正整数
对一切正整数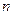 ,
,总有
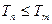 ,此时
,此时 或
或 ……………………………..(13分)
……………………………..(13分)略

练习册系列答案
相关题目
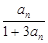 ,a1=2,则a4为 ( )
,a1=2,则a4为 ( )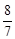
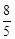
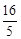
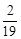
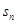 ,
,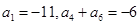 ,则当
,则当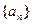 的前n项和为
的前n项和为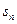 ,
,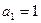 且满足
且满足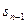 +n (n>1且n
+n (n>1且n ∈
∈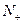 )
)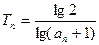 ,求使得不等式
,求使得不等式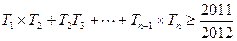 成立的最小正整数n的值
成立的最小正整数n的值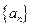 中,
中,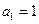 ,前
,前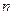 项和
项和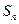 满足条件
满足条件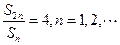 ,
,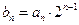 ,求数列
,求数列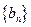 的前
的前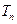 .
.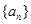 为等差数列,
为等差数列,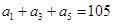 ,
,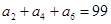 ,则
,则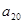 等于( )
等于( )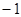
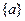 中,
中,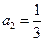 ,公比
,公比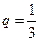 。
。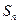 为
为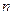 项和,证明:
项和,证明: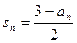
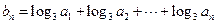 ,求数列
,求数列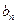 的通项公式.
的通项公式. 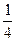 (an+1)
(an+1)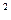 (n∈N*).
(n∈N*).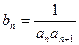 ,记数列{bn}的前n项和为
,记数列{bn}的前n项和为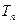 ,求
,求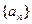 是等差数列,其前n项和为
是等差数列,其前n项和为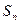 ,已知
,已知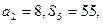
 式; (2)设
式; (2)设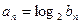 ,证明
,证明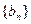 是等比数列,并求其前n项和
是等比数列,并求其前n项和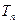 。
。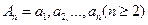 满足
满足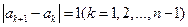 ,数列
,数列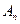 为
为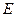 数列,记
数列,记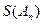 =
=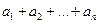 .
.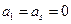 ,且
,且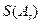 〉0的
〉0的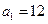 ,n=2000,证明:E数列
,n=2000,证明:E数列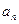 =2011;
=2011;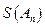 =0?如果存在,写出一个满足条件的E数列
=0?如果存在,写出一个满足条件的E数列