题目内容
已知函数 (kÎ(0,+¥),a>1>b>0)的定义域恰为区间,是否存在这样的a、b使得f(x)恰在(1,+¥)上取正值,且f(3)=lg4?若存在,求出a、b的值;若不存在,请说明理由.
(kÎ(0,+¥),a>1>b>0)的定义域恰为区间,是否存在这样的a、b使得f(x)恰在(1,+¥)上取正值,且f(3)=lg4?若存在,求出a、b的值;若不存在,请说明理由.
答案:略
解析:
提示:
解析:
|
本题涉及字母参数较多,因此,根据题设条件减少字母参数是解决本题的关键.同时,在审题时,要深刻理解题设中两个“恰”字的含义,从而列出关于 a、b、k的方程,解方程即可.解:∵ 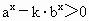 ,∴ ,∴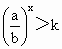 . .
即 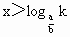 为其定义域满足的条件,于是由 为其定义域满足的条件,于是由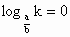 得k=1,从而 得k=1,从而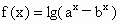 . .
∵易证 f(x)在(1,+¥ )上是增函数.∴当 x>1时,f(x)>f(1).又 f(x)恰在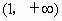 上取正值, 上取正值,
∴ f(1)=0,即a-b=1.又 f(3)=lg4,∴ . .
又 a>1>b>0,解得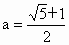 , ,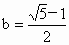 . . |
提示:
|
对于存在性问题,通常解法是:首先默认满足题意的实数存在,然后根据题设条件进行求解,如果求解合理且能求出满足题设的实数,则表明存在;否则,不存在. |

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
已知函数f(x)=2x2-kx-9在[5,20]上有单调性,则实数k的取值范围为( )
| A、(-∞,20] | B、[80,+∞) | C、(-∞,20]∪[80,+∞) | D、(-∞,-80]∪[-20,+∞) |