题目内容
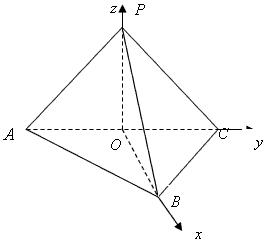
如图,在三棱锥-P-ABCD中,平面ABC⊥平面APC,AB=BC=AP=PC=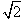 ,∠ABC=∠APC=90°,
,∠ABC=∠APC=90°,
(1)求直线PA与平面PBC所成角的正弦值;
(2)若动点M在底面三角形ABC上,二面角M-PA-C的余弦值为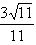 ,求BM的最小值。
,求BM的最小值。
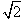 ,∠ABC=∠APC=90°,
,∠ABC=∠APC=90°,(1)求直线PA与平面PBC所成角的正弦值;
(2)若动点M在底面三角形ABC上,二面角M-PA-C的余弦值为
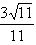 ,求BM的最小值。
,求BM的最小值。 
|
解:(1)取AC中点O,因为AB=BC, |
 |

练习册系列答案
相关题目
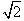 ,
,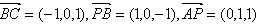 ,
,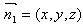 ,
,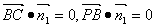 得方程组
得方程组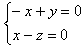 ,
,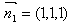 ,
,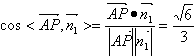 ,
,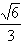 。
。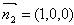 ,
,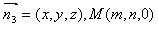 ,
,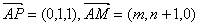 ,
,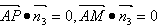 ,
,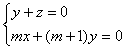 ,
,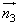
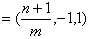 ,
,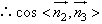
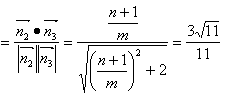 ,
,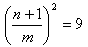 ,
,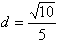 。
。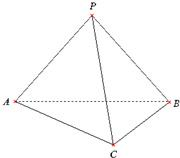 如图,在三棱锥P-ABC中,PA=PB,PA⊥PB,AB⊥BC,∠BAC=30°,平面PAB⊥平面ABC.
如图,在三棱锥P-ABC中,PA=PB,PA⊥PB,AB⊥BC,∠BAC=30°,平面PAB⊥平面ABC.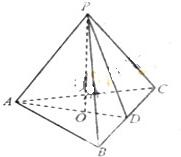 如图,在三棱锥P-ABC中,AB=AC,D为BC的中点,PO⊥平面ABC,垂足O落在线段AD上.
如图,在三棱锥P-ABC中,AB=AC,D为BC的中点,PO⊥平面ABC,垂足O落在线段AD上. 如图,在三棱锥P-ABC中,
如图,在三棱锥P-ABC中,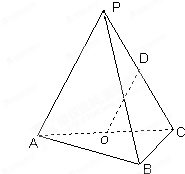 如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,AB⊥BC,AB=BC=PA=PC,点O、D分别是AC、PC的中点.
如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,AB⊥BC,AB=BC=PA=PC,点O、D分别是AC、PC的中点. 如图,在三棱锥P-ABC中,PA⊥底面ABC,∠ABC=90°,PA=AB=BC=1,则PC与底面ABC所成角的正切值为
如图,在三棱锥P-ABC中,PA⊥底面ABC,∠ABC=90°,PA=AB=BC=1,则PC与底面ABC所成角的正切值为